|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| Englische Version |
5 - Der Ansatz zum Grundfeld
5.1 - Grundschwingungen
| Aufgrund der bisherigen Betrachtung liegt
der Schluss nah, dass das Magnetfeld der Erde eine
symmetrische Struktur bzgl. eines dreiachsigen Ellipsoids
besitzt. In dieser Struktur treten bestimmte Winkel auf,
die ganzzahlige Teile von 360 Grad sind. Sieht man einmal von den eigentlichen felderzeugenden Elementen im Erdinneren ab und konzentriert sich lediglich auf das äußere, die Erde umspannende Feld, so lässt das folgenden Ansatz zu: Das Gesamtfeld der Erde lässt sich, nach dem Huygenschen Prinzip (Huygens - niederländischer Physiker, 1629-1695), mittels eines Spektrums diskreter Frequenzen und global fixierter „Quellpunkte“ erklären. Und zwar als Summe einer Menge von stehenden räumlichen Wellen, den sogenannten Grundschwingungen (Elementarwellen). Diese breiten sich von den „Quellpunkten“ aus, und durch Überlagerung aller Grundschwingungen entsteht - als stationärer Zustand - das Erdfeld. |
| Der
Ansatz erfolgt auf der Basis von Schwingungen auf bzw.
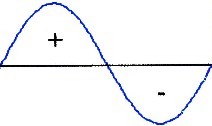
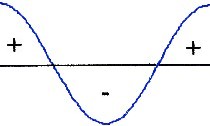
um eine Kugel Beispiele für Schwingungsmöglichkeiten: |
 |
 |
 |
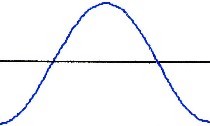| Sinus | Kosinus |
| Sinus bzw. Kosinus = Schwingung = Welle |
| Für
physikalische Schwingungen gilt: Formel: f·λ = c (Frequenz mal Wellenlänge gleich Lichtgeschwindigkeit) |
5.2 - Das Modell
| Um die eigentlichen Quellpunkte des Feldes und der Grundschwingungen zu bestimmen, bedarf es, wie schon erwähnt, einer 2-dimensionalen Fourier-Analyse (siehe Kapitel 8). Zur Veranschaulichung genügt hier aber zunächst ein qualitativer Ansatz: | ||
 |
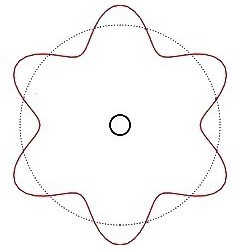Man stelle sich eine Kugel vor, um die herum
sich eine stehende Welle gebildet hat. Analog zum
Bohrschen Atommodell, d.h. wenn man nach De Broglie das
umlaufende Elektron als Welle auffasst. Es passen nur ganzzahlige Schwingungen (n?N) um die Kugel: n · λ ~ 360° = 2π |
|
| Abbildung 5.1 - Grundschwingung | ||
 |
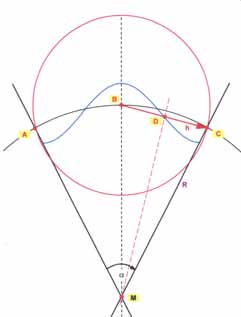Die Wellenlänge ist proportional zum
Kreiswinkel Α: λ ~ α |
|
| Abbildung 5.1.1 - Grundschwingung und Winkel |
| Bedingung für n Schwingungen um eine Kugel: | n · α = 2π |
| Eine stehende Welle um eine Kugel lässt
sich physikalisch als stationärer Zustand
interpretieren Eine Kugel besitzt 3 Freiheitsgrade Zur
Veranschaulichung: Als Quellpunkt dient der Nordpol
(Abb.5.1). Lässt man die Grundschwingung von Nordpol
über Südpol wieder zum Nordpol laufen, so ergibt sich
die zweite Welle um den Äquator herum. Für diese ersten
beiden Schwingungen existiert ein mathematisches Konzept,
dass sich für eine Darstellung eignet, nämlich die Kugelflächenfunktionen.
|
5.3 - Kugelflächenfunktionen
| Stehende Wellen auf einer Kugeloberfläche werden als Kugelflächenfunktionen bezeichnet. Es existieren 3 Arten von Schwingungsformen. (Siehe dazu z.B. auch Torges „Geodäsie“, Seite 41-43.) | ||
 |
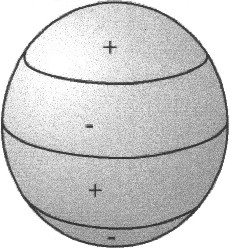Zonale
Kugelflächenfunktionen hängen lediglich vom Breitengrad ab sin φ cos φ |
|
| Abbildung 5.2 - zonale Kugelflächenfunktionen | ||
 |
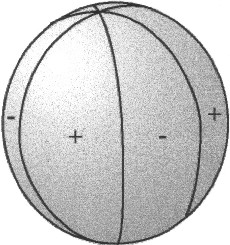Sektorielle
Kugelflächenfunktionen hängen lediglich vom Längengrad ab sin λ cos λ |
|
| Abbildung 5.3 - sektorielle Kugelflächenfunktionen | ||
 |
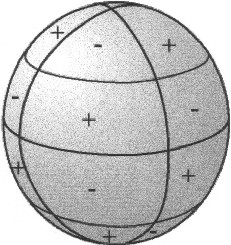Tesserale
Kugelflächenfunktionen hängen vom Breitengrad und vom Längengrad ab sinφ·sinλ sinφ·cosλ cosφ·sinλ cosφ·cosλ |
|
| Abbildung 5.4 - tesserale Kugelflächenfunktionen | ||
5.4 - Überlagerung von Sinuswellen
| Kugelflächenfunktionen lassen sich als zwei Sinus - bzw. Cosinuswellen darstellen, die senkrecht aufeinander stehen und sich multiplikativ überlagern. Zwei solcher Wellen lassen sich nach folgenden qualitativen Regeln addieren: | ||
 |
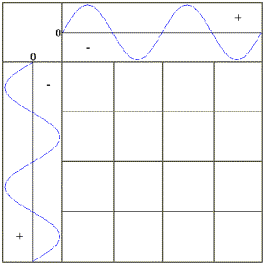Die Nullpunkte der beiden Wellen werden auf die Betrachtungsebene übertragen So erfolgt die Bildung des Null-Gitters | |
| Abbildung 5.51 Null-Gitter zweier Sinuswellen | ||
 |
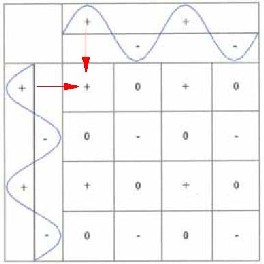1) + und + ergibt + 2) - und - ergibt - 3) + und - ergibt 0 Wie zu sehen ist, ergeben sich Felder mit verschiedenen Vorzeichen bzw. verschiedenen Zuständen. Es existieren drei Schwingungszustände: positiv(+), negativ(-), neutral(0) |
|
| Abbildung 5.5 - Addition zweier Sinuswellen | ||
 |
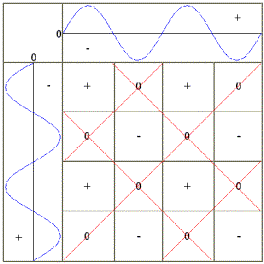Auffallend
ist, dass alle Nullfelder diagonal zueinander
liegen. Verbindet man nun die Nullfelder miteinander, so
ergibt sich das nebenstehende Bild. Im weiteren Verlauf
wird dieses gitterartige (rote) Schwingungsgefüge als Grundfeld oder Gitter bezeichnet. |
|
| Abbildung 5.6 - Entstehung des Grundfeldes | ||
5.5 - Das Grundfeld
| Überlagert man zwei Sinuswellen, die senkrecht aufeinander stehen, quantitativ so ergeben sich die folgenden Abbildungen 5.8 und 5.9. Deutlich zu erkennen sind die exakte Gitterbildung, sowie die abwechselnde Polarität der einzelnen Felder. |
 |
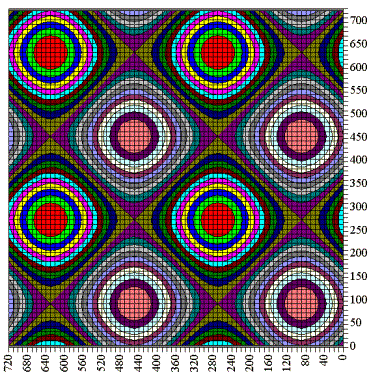Die Überlagerung zweier - senkrecht
aufeinander stehenden - Wellen ergibt das bekannte
Gittermuster mit den abwechselnden Polaritäten der
Gitterfelder. (Abbildung 5.8 und 5.9) Hier zeigt sich, dass die Feldmaxima in der Mitte der Quadrate punktförmig auftreten, während die Linien aus Nullwerten bestehen - analog zu den Chladni-Klangfiguren. |
|
| Abbildung 5.8 - Das Grundfeld | ||
 |
Mathematisch
gesehen lassen sich Grundfelder bzw. tesserale
Kugelflächenfunktionen durch die Multiplikation
zweier Sinus bzw. Kosinuswellen darstellen. Es entstehen so Terme, wie sie in der Gleichung von Gauß und Weber (Kapitel 2.7) auftreten. Siehe dazu auch Kapitel 10.3 |
|
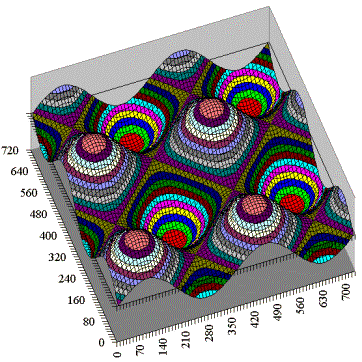
| Abbildung 5.9 - Die Intensität des Grundfeldes in 3D-Sicht |
| Grundfeld = Gitter = zweidimensionales Schwingungsgefüge |
| Gut zu
sehen ist in Abbildung 5.9 auch, dass jeweils zwei
erzeugte Gitterfelder wiederum eine (erzeugte) Schwingung
ergeben. Dies erlaubt zwei Sichten des Gitters: 1) Das erzeugte Gitter wird in der Ebene der Grundschwingungen beschrieben 2) Das erzeugte Gitter wird in der Gitterebene selber beschrieben |
| Möglich ist hier noch ein zweites Gitter einzuzeichnen. Und zwar das Maximalgitter: Es verbindet die Feldmaxima (Minima) miteinander und stellt den extremalen Verlauf des Feldes dar. |
| Da sich ein komplettes streckenmässig quadratisches Gitter auf einer Kugel nicht verwirklichen lässt, entstehen Schwingungssysteme, die gestaltet sind wie das geographische Gittersystem. Es existieren immer zwei Pole. Die zugehörigen "Meridiane" und "Breitenkreise" bilden dann das Gittersystem. |
| Durch den Sonnensatteliten Soho sind Bilder auf Radarbasis entstanden, die eindeutig Grundfelder bzw. tesserale Kugelflächenfunktionen auf der Sonnenoberfläche zeigen. Da erhebt sich die Frage ob das Magnetfeld der Erde nicht auch solche Schwingungsstrukturen ausgebildet hat. |
| Anfang der 50er Jahre im vorigen Jahrhundert beschrieb Dr. med. Ernst Hartmann ein Gittersystem, welches in der magnetischen Nord-Süd Richtung verläuft. Dieses Hartmann-Gitter wird im Kapitel 11 ausführlicher behandelt. Mit dem Grundfeldmodell ist nämlich ein Ansatz gegeben, das Hartmann-Gitter als magnetische tesserale Kugelflächenfunktion zu beschreiben. |
 |
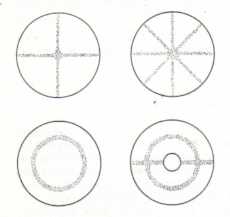Ein Analogon zum Grundfeld bilden hier die Chladni-Klangfiguren.
Bestrahlt man eine sandbeschichtete Platte mit
Schallwellen, so entstehen im Resonanzfall stehende
Wellen auf der Platte. Entlang der Nullwerte bleibt der Sand dann liegen und es entstehen die typischen Schwingungsfiguren. (siehe dazu auch in „Physik“ von Gerthsen, Kneser, Vogel – Kapitel 4.1.5 – Eigenschwingungen deformierbarer Körper) |
|
| Abbildung 5.7 - Chladni - Figuren |
| Die Überlagerung zweier Sinuswellen lässt sich dreidimensional auch wie in Abbildung 5.10 darstellen |
|
Abbildung 5.10 - Grundschwingungen und Grundfeld |
| Während der mathematische Begriff der Kugelflächenfunktion nicht nach der Ursache des Schwingungsfeldes fragt, so müssen bei der physikalischen Betrachtung die zugrunde liegenden Wellen mit einbezogen werden. Dies leistet der Begriff des Grundfeldes. Das Grundfeld ist durch die Grundschwingungen definiert. |
| Die
Bezeichnung Grundfeld oder Gitter ist als physikalisches
Äquivalent zum Begriff der mathematischen tesseralen Kugelflächenfunktion zu sehen |
Tesserale Kugelflächenfunktionen = Produkt zweier Schwingungen = 2 senkrecht aufeinander stehende Wellen = Gitter = Grundfeld = zweidimensionales Schwingungsgefüge |
5.6
- Huygensches Prinzip
(Ergänzung
zum Buch)
| Nach Kapitel 5.2 besitzt eine Kugel 3 Freiheitsgrade. Durch die Verwendung von Kugelflächenfunktionen wären 2 Freiheitsgrade abgedeckt. Fehlt noch der dritte Freiheitsgrad, also die radiale Richtung. Dazu wird das Verständnis einer physikalischen Darstellung benötigt mit dem sich die Ausdehnung physikalischer Wellen beschreiben lässt: das Huygensche Prinzip. |
 |
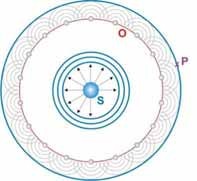Das Huygensche Prinzip geht von einer Quelle
S aus, die gleichförmig Wellenfronten nach allen
Seiten hin erzeugt. Um die resultierende Wellenfront im Punkt P zu erhalten ist es aber nicht notwendig die gesamte Ausbreitung von S aus zu betrachten. |
 |
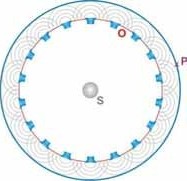Das Huygensche Prinzip sagt aus, dass
jeder Punkt (O) einer Wellenfront als Ausgangspunkt einer
neuen Welle, der so genannten Elementarwelle (grau),
betrachtet werden kann. Die Lage der resultierenden Wellenfront (P) ergibt sich durch Überlagerung (Superposition) sämtlicher Elementarwellen |
| Die Wellenursprünge (O) liefern durch Superposition der Elementarwellen die resultierende Wellenfront (P). In drei Dimensionen sind Elementarwellen kugelförmig, in zwei Dimensionen kreisförmig. |
 |
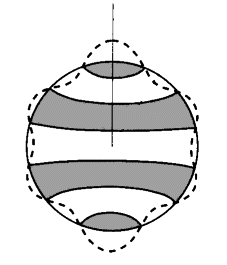Welle um eine Kugel: Extremwerte der Welle = Quellen = Wellenursprünge 1 Schwingung = 2 Quellen |
 |
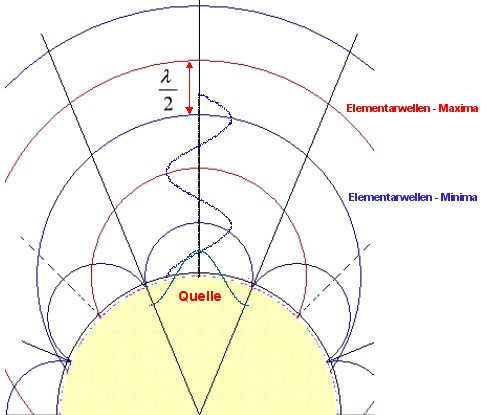Schwingungszustand für eine
Schwingung nach dem Huygenschen Prinzip mit einem Maximum (Wellenberg) als Quelle (grün) Die Minimalfronten (blau) und die Maximalfronten (rot) sind dabei die Elementarwellen |
| In der vorherigen Abbildung ist die Schwingungssituation im Querschnitt für eine Schwingung dargestellt. In der folgenden Abbildung ist die Schwingungssituation für n Schwingungen dargestellt. |
 |
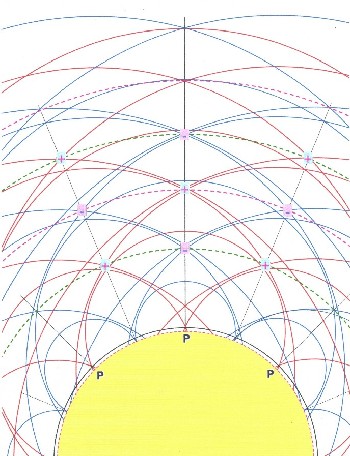Von den Quellpunkten P ausgehend,
bilden sich, nach dem Huygenschen Prinzip, um
jeden Quellpunkt konzentrische Kreise (Elementarwellen)
von Minimalzonen (rote Kreise) und Maximalzonen
(blaue Kreise) aus. Da ein stationärer Zustand besteht, sind die Wellenfronten in der räumlichen Lage feststehend. Die Superposition der Elementarwellen erfolgt nach den selben Regeln wie schon in Kapitel 5.4 beschrieben. |
| Durch die
Interferenz also Überlagerung von positiven
Wellenfronten entstehen Schwingungsmaxima (mit
plus gekennzeichnet) und im folgenden als Plus-Pole
bezeichnet Durch die Interferenz also Überlagerung von negativen Wellenfronten entstehen Schwingungsminima (mit minus gekennzeichnet) und im folgenden als Minus-Pole bezeichnet und zwar da, wo mehrere Wellenfronten einen Schnittpunkt bzw. ein Ballungszentrum bilden Durch die Superposition von positiven und negativen Elementarwellen bilden sich auch Nullpole Die durch die Superposition entstandenen Schwingungsextrema liegen wiederum auf Kugeloberflächen (gestrichelt gezeichnete Kreise) die die erzeugende Kugel (z.B. die Erde) konzentrisch einhüllen, im folgenden Schichten = L genannt Zwischen diesen Extremalschichten entstehen Nullpole die ebenfalls auf konzentrischen Kugelschalen liegen - im folgenden Nullwände genannt |
 |
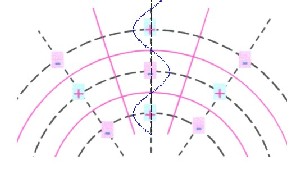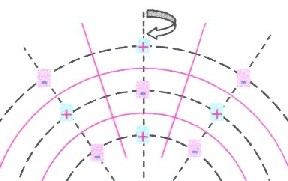
Es ergibt sich diese vereinfachte Sicht des
resultierenden Feldes: Schwarze gestrichelte Linien = Extremal-Linien = Schichten Magenta Linien = Null-Linien = Nullwände Die erzeugten Schichten L bilden eine radiale stehende Welle |
| Die mathematisch, physikalische Ermittlung der Schichten, also die quantitative Bestimmung, erfolgt in Kapitel 12 |
5.7
- Schichtungsgefüge, Schwingungsgefüge
(Ergänzung
zum Buch)
| Eine stehende Welle auf einer Kugel erzeugt ein rotationssymmetrisches räumliches Gefüge: |
 |
|
| Die Pole liegen kreisförmig
auf konzentrischen Kugelschalen Die Nullwände bilden konzentrische Kegel und konzentrische Kugelschalen |
 |
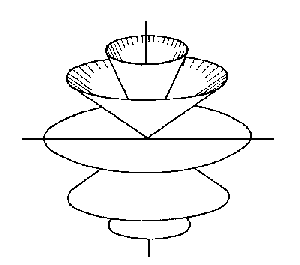| Schichtungsgefüge = von einer stehenden Welle erzeugte radiale Schichtungsstruktur |
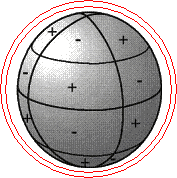
| Zwei stehende Wellen auf einer Kugel erzeugen ein radiales gitterförmiges Gefüge: |
 |
 |
 |
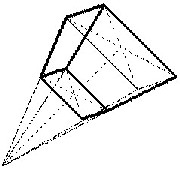| Es ergeben sich zwei Sichtmöglichkeiten: |
| Die Nullflächen bilden die Wände
eines gitterförmigen radialen Schwingungssystems Die Pole liegen im Mittelpunkt des jeweils einhüllenden Null-Quaders |
 |
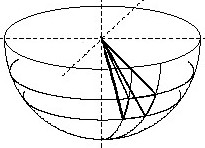
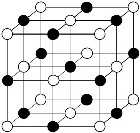
| Die Pole bilden ebenfalls ein
gitterförmiges radiales Schwingungssystem ähnlich einem
molekularem Gitter (z.B. NaCl) im folgenden Polgitter
genannt Die Polverbindungen verhalten sich wie Stäbe, die an beiden Enden frei schwingen |
 |
| Raum-Gitter = von zwei stehenden Wellen erzeugtes radiales Schichtungsgefüge |
| Schwingungsgefüge = Summe aller möglichen Raum-Gitter auf einer Kugel |
| Bemerkung: Das von einer Welle erzeugte Schichtungsgefüge ist identisch mit dem Schichtungsgefüge das von zwei Wellen erzeugt wird. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
