|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| Englische Version |
17 - Zur Gestalt der Erde
17.1 - Geodätische Systeme
| Geodätische Systeme stellen Näherungsmodelle der Erdgestalt dar. Ausgehend von einem Rotations - Ellipsoiden versuchen solche Systeme Parameter zu definieren, die eine immer genauere Beschreibung der Erde in ihrer 3-dimensionalen Ausdehnung erlauben. | ||
 |
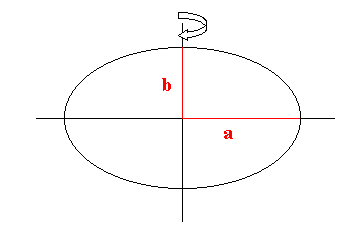Ausgangspunkt ist, in der Regel, eine
Ellipse mit der großen Halbachse a und der kleinen
Halbachse b. Lässt man nun die Ellipse um die kleinere
Achse rotieren, so entsteht ein sogenanntes
Rotationsellipsoid, welches auch als Sphäroid
bezeichnet wird. Bei genügend hoher Genauigkeit der Beobachtung, stellt sich allerdings heraus, dass ein ellipsoidisches Erdmodell als exakte Lösung nicht ausreichend ist. |
|
| Abbildung 17.1 - Entstehung eines Rotationsellipsoids | ||
| Die Figur der Erde wird durch eine physische
und durch eine mathematische Oberfläche beschrieben.
Unter der physischen Erdoberfläche versteht man die
Begrenzung zwischen festen und flüssigen Erdmassen
gegenüber der Atmosphäre. Hier findet ja sozusagen ein
Dichtesprung im Aufbau der Erde statt, und zwar von der
mittlere Dichte der oberen Erdkruste mit r = 2,7 gcm-3
auf die Luftdichte mit r = 0,0013 gcm-3. Die unregelmäßig gestaltete Oberfläche der festen Erdmassen wie z.B. die Kontinente lässt sich aber nicht so ohne weiteres durch eine mathematische Beziehung darstellen. Hier hilft nur die Punktweise Erfassung und Kartographierung. Üblicherweise geschah dies in 5° x 5° oder auch in 1° x 1° Unterteilungen. Die
Oberfläche der Ozeane, die immerhin etwa 70% der
Erdoberfläche ausmachen, weist jedoch ein Bildungsgesetz
auf. Unter bestimmten Vorraussetzungen bilden die Meere
eine Fläche, auf der ein konstantes Schwerepotential
herrscht. Sie ist dann Niveaufläche des Erdschwerefeldes |
|
| Abbildung 17.2 - Geoid |
| Die Erde
ist aufgebaut aus Massen unterschiedlicher Dichte, die
allerdings nicht gleichmäßig heißt homogen verteilt
sind. Daher kann es lokal vorkommen, das die physische
(gemessene) Lotrichtung nicht mit der Ellipsennormalen
übereinstimmt. Diese Lotabweichungen müssen mit
berücksichtigt werden. Diese Abweichungen werden als Geoidundulationen bezeichnet. Daher wird, in der Regel, ein Referenzellipsoid angenommen, und die auftretenden Höhen über der Ellipsoidoberfläche aufgetragen. |
| Bei den bis
heute getätigten Geoidbestimmungen hat sich gezeigt, das die Abweichungen des Geoids von einem mittleren Rotationsellipsoiden kleiner als 100 Meter in der Höhe betragen. |
 |
Um eine, noch bessere Anpassung an den Geoid
zu erhalten, als ein zweiachsiges Rotationsellipsoid,
wäre geometrisch gesehen, der nächste Schritt, es mit
einem dreiachsigen, also echtem Ellipsoiden zu versuchen.
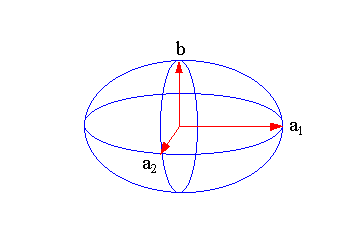
In der Abbildung 17.3 ist ein solcher Ellipsoid
dargestellt. Bezogen auf die Erde ist dann a1 dabei die große Äquatorhalbachse, a2 die kleine Äquatorhalbachse und b die Polachse. |
|
| Abbildung 17.3 - (echter) dreiachsiger Ellipsoid | ||
| Es sind mehrfach Versuche unternommen
worden, die Parameter für ein dreiachsiges Ellipsoid als
Erdmodell zu bestimmen. Die Ergebnisse sind jedoch voneinander different, und zwar wegen der unterschiedlichen Verteilung der Beobachtungen auf der Erdoberfläche und den verschiedenen Methoden die bei der Reduktion auf das Ellipsoid angewandt wurden. |
| Mit Hilfe der Satellitengeodäsie sind, 1966 durch C.A. Lundquist und G. Veis, folgende Parameter ermittelt worden: |
| a1-a2
= 69 Meter λo = -14° 45` (westliche Länge) |
| a1 ist dabei die
große Äquatorhalbachse, a2 die kleine
Äquatorhalbachse und λo die geographische
Länge der großen Halbachse. Nimmt man nun den Wert von Lundquist und Veis, und vergleicht diesen mit dem Nullpunkt (-13,5 Grad als geographische Längenposition-siehe Kapitel 4 Winkelansatz) so lässt sich, global gesehen, eine gute Übereinstimmung feststellen. |
| Da die Abweichungen des zweiachsigen
Rotationsellipsoiden vom Geoid, in der Regel, in
derselben Größenordnung liegen wie die Achsendifferenz
von 69 Meter, wird eine wesentlich bessere Anpassung an
das Geoid durch ein dreiachsiges Ellipsoid eigentlich
nicht erreicht. Andererseits dagegen werden geodätische Berechnungen durch eine kompliziertere Geometrie des Ellisoids ziemlich erschwert. Auch als geophysikalische Normalfigur ist das dreiachsige Ellipsoid schlechter geeignet, da sich mit den Werten für die Erdmasse und der Winkelgeschwindigkeit der Erde eine unnatürliche Form ergibt. Das dreiachsige Ellipsoid hat sich daher als Bezugskörper in der heutigen Geodäsie nicht durchgesetzt. |
| Genau genommen rangieren das mittlere
Rotationsellipsoid bzw. das Geoid und das dreiachsige
Ellipsoid, bzgl. der Abweichungen der tatsächlichen
Erdgestalt, in derselben Größenordnung. Sie sind dem zufolge auch gleichwertige Modelle. |
17.2 - Die Mittelwertpunkte der Erde
| Wertet man alle Mittelwerte aus, die an
einer Ellipse, bezüglich der Achsen, möglich sind, so
ergeben sich fünf Fälle. Diese sind in der folgenden Tabelle aufgeführt. Die Werte sind dabei gerundet, da alle Mittelwerte lediglich ein paar Bogensekunden bzw. Bogenminuten von den angegebenen Zahlenwerten abweichen. Die Art der Mittelwertbildung ist dabei beliebig. Daher wird hier nicht mehr zwischen den einzelnen Mittelwerten unterschieden, sondern die Mittelwerte allgemein mit M bezeichnet. |
| FALL | Mittelwertbedingung | Winkel |
| I | R=M | 45° |
| II | y=M/2 | 30° |
| III | x=M/2 | 60° |
| IV | x=M | 3° |
| V | y=M | - |
| Bemerkenswert ist, das für y=M keine Mittelwerte existieren, da alle Mittelwerte größer als die kleine Halbachse sind und daher außerhalb der Ellipse liegen. Zeichnet man alle vorhandenen Mittelwerte in die Ellipse ein, so ergibt sich folgende Abbildung 17.4: |
 |
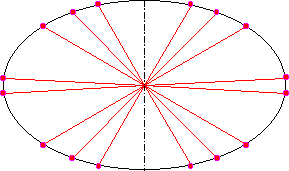| Abbildung 17.4 - Ellipse und ihre Mittelwerte |
| Nimmt man als Erdmodell ein Rotationsellipsoid,
so ergeben die Mittelwerte aus der Abbildung ausgezeichnete
Breitengrade. Nimmt man ein dreiachsiges Ellipsoid als Erdmodell (Werte von Lundquist und Veist), so ergeben sich einzelne Punkte. Diese Punkte werden ab jetzt als Mittelwertpunkte bezeichnet. Trägt man alle Mittelwertpunkte in eine Zeichnung der Erde ein, so ergibt sich die nächste Abbildung |
 |
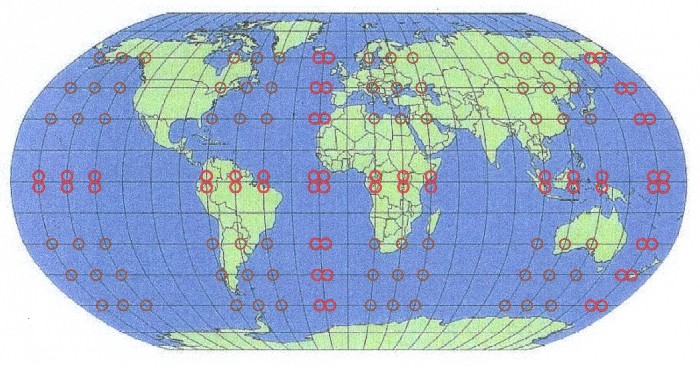| Abbildung 17.5 - Erde und Mittelwertpunkte |
| Eine geodätische Betrachtung der Mittelwertpunkte lässt sich unter "Die Gestalt der Erde-13" nachschlagen. Eine Ableitung der Mittelwertpunkte lässt sich unter "Die Gestalt der Erde-12" nachsehen. |
| Ein
Teil der Mittelwertpunkte der Erde verfügen über einen
erstaunlichen Zusammenhang mit dem Wasserverlauf der Erde.
Wasservorkommen lassen sich an folgenden Mittelwertpunkten finden: Südamerika-Amazonasbecken, Nordamerika-Ontario-See, Nordeuropa-Ladoga-See, Afrika-Victoria-See, Asien-Chanka-See, Australien-zwei Gebiete mit mehreren Seen. Die wichtigsten Flussdeltas, die auf Mittelwertpunkten liegen sind: Po-Delta, Donau-Delta und Wolga-Delta in Europa und direkt darunter das Nil-Delta und das Euphrat/Tigris-Delta. Sowie in Südamerika Rio de la Plata und Amazonas-Delta, in Nordamerika der Hudson Bay und in Asien das Jangtse –Delta. Ferner sind in Europa das Adriatische Meer, das Schwarze Meer und das Kaspische Meer mit Mittelwertpunkten assoziiert, sowie der bottnische Meerbusen. Interessant ist auch die Lage des Mittelmeeres zwischen den Mittelwertpunkten. Zwischen zwei Mittelwerten liegt auch der Baikal-See in Asien |
| Die Fluss-Deltas liefern hier quasi die Antwort. Da Wasser stets abwärts fließt, müssen die Flussdeltas niedriger als die Umgebung liegen. Und das bedeutet: |
| Die
Mittelwertpunkte, stellen bezüglich der Landmassen die niedrigsten Punkte auf der Erdoberfläche dar. |
17.3 - Magnetfeld und Mittelwertpunkte
| Hier interessiert noch die Lage der
magnetischen Extremwerte aus Kapitel 2 bezüglich der Mittelwertpunkte.
Und das führt zur nächsten Zeichnung 17.6. Die
magnetischen Kerngebiete der Extrema des Gesamtfeldes
sind hier gelb eingezeichnet und die eigentlichen
Extremwerte darin rot umrandet. Wie zu sehen treten die magnetischen Extrema nur an den Rändern der Mittelwertgebiete auf. Und alle Extrema liegen auf sogenannten ausgezeichneten Breitengraden (rote Linien), die sich aus der Schmiegkreis-Konstruktion und dem zugehörigen harmonischen Mittel der Ellipsoidachsen ergeben. Die Schmiegekreise spielen bei der Ellipse eine besondere Rolle. Einerseits kann mit ihnen die Ellipse relativ schnell konstruiert werden. Andererseits werden die Radien der Schmiegekreise, speziell der kleinere Radius, benutzt, um die Ellipse in ihren Eigenschaften zu beschreiben, z.B. für die Ellipse als Kegelschnitt. Ausgehend von einem Rotationsmodell für die Erde, heißt von einem beliebigen geödätischen System, entstehen durch die Schmiegkreis-Konstruktion vier ausgezeichnete Breitengrade. |
| φ12
= ±29° 58′ 19-20,5″ φ34 = ±59° 58′ 19-20,5″ |
| Innerhalb der Grenzen von 19-20,5 Bogensekunden liegen die Werte aller bekannten geodätischen Systeme. |
 |
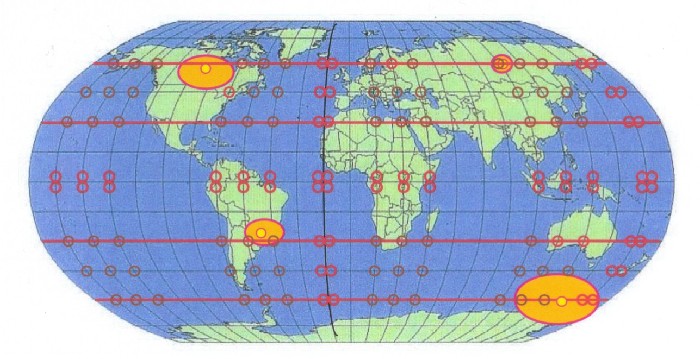| Abbildung 17.6 - Erde, Mittelwertpunkte und magnetische Extrema |
| Die magnetischen Extrema treten nur an den Rändern der Mittelwertgebiete auf. Und alle Extrema liegen auf den ausgezeichneten Breitengraden (rote Linien), die sich aus der Schmiegekreis- Konstruktion und dem harmonischen Mittel ergeben. |
| Das
harmonische Mittel der Ellipsoidachsen nimmt eine
besondere Stellung bezüglich der Ellipse ein. Es
existiert nämlich ein Zusammenhang mit der
Schmiegkreis-Konstruktion, auf den hier aber nicht näher
eingegangen wird. Durch das harmonische Mittel der Ellipsoidachsen entstehen zwei weitere ausgezeichnete Breitengrade. |
| φ56 = ±30° 08′ 17,6-24,5″ |
| φ56
und φ12 liegen lediglich 10
Bogenminuten auseinander und sind bei einer globalen
Darstellung (wie in Abbildung 17.6) nicht mehr
auseinander zu halten. Innerhalb der Grenzen von 17,6-24,5 Bogensekunden liegen die Werte aller bekannten geodätischen Systeme. |
| siehe dazu "Die Gestalt der Erde-10" und "Die Gestalt der Erde-11" |
| Aus den Zeichnungen und den Betrachtungen lässt sich dann folgender Schluss ziehen, wenn man ein dreiachsiges Ellipsoid zugrunde legt: |
| Die Lage der magnetischen Extremwerte des
Gesamtfeldes stehen in Relation zu den Mittelwertpunkten und den ausgezeichneten Breitengraden |
17.4 - Magnetfeld und dreiachsiges Ellipsoid
| Trägt
man nun alle gefundenen magnetischen Extrema und Punkte,
sowie die ausgezeichneten Breitengrade, in eine
Gesamtkarte der Totalintensität ein, so ergibt sich
Abbildung 17.7, die quasi eine Erweiterung von Bild 11.6
darstellt. Die blauen Senkrechten in Bild 17.7 stellen die Achsen eines dreiachsigen Ellipsoid dar, mit einer 22,5 Grad Teilung. Die roten Senkrechten orientieren sich am Hauptmeridian des magnetischen Schwingungssystems, ebenfalls mit einer 22,5 Grad Teilung. Gut zu erkennen ist, das sich Ellipsoidsystem und magnetisches System nur geringfügig voneinander unterscheiden, also sozusagen in Phase zu einander liegen. Die Hauptachse des dreiachsigen Ellipsoid liegt, nach Lundquist und Veis, bei –14,75 Grad West. Der Hauptmeridian des magnetischen Systems liegt bei –83,5 Grad West. Daraus ergibt sich eine Differenz von 1,25 Grad zwischen den beiden Systemen. Die ist auch die Differenz zwischen dem Wert von Lundquist und Veis, und dem Nullpunkt aus Kapitel 4.4. Global gesehen stimmen beide Systeme somit gut überein. |
 |
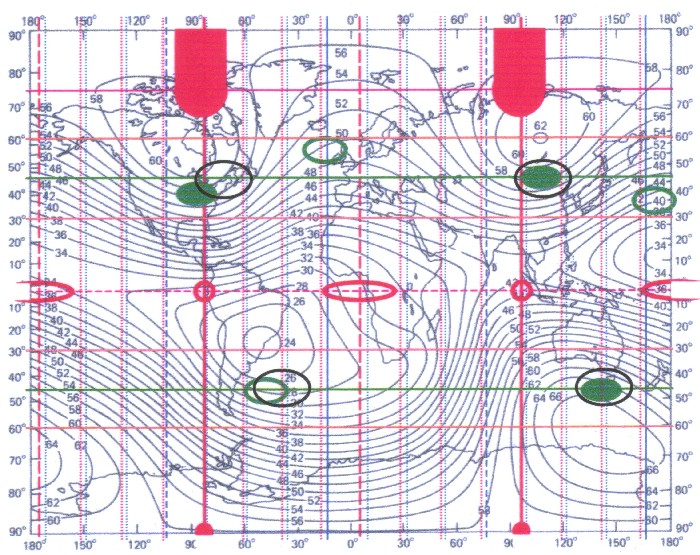| Abbildung 17.7 - Magnetfeld und dreiachsiger Ellipsoid |
| Aus der Zeichnung 17.7 lässt sich dann folgender Schluss ziehen: |
| Die Lage
aller magnetischen Extrema der Erde steht in Relation zu einem dreiachsigen Ellipsoiden |
| Aus den Zeichnungen 17.5 bis 17.7 dieses Kapitels und den bisherigen Betrachtungen, hauptsächlich aus den Kapitel 4.4, Kapitel 9.5 und Kapitel 13, lässt sich dann folgender Schluss ziehen, wenn man ein dreiachsiges Ellipsoid zugrunde legt: |
| Die Lage
der magnetischen Extrema der Erde steht in Relation zur Gestalt der Erde |
17.5 - Das C-Gitter
| Basierend
auf der Vierer-Struktur des sektoriellen Anteils,
entsteht um den Äquator herum eine Teilung von 22,5 Grad
(in Kapitel 9). Durch die ausgezeichneten Breitengrade und die 45 Grad des tesseralen Systems bzw. der Quellpunkte bedingt, ergibt sich von Nord nach Süd eine 15 Grad Teilung. Damit lässt sich das bestehende B-Gitter noch etwas verfeinern. Einzeichnen aller Breiten und Längen mit den beiden Teilungen 15 und 22,5 Grad ergibt das C-Gitter: |
 |
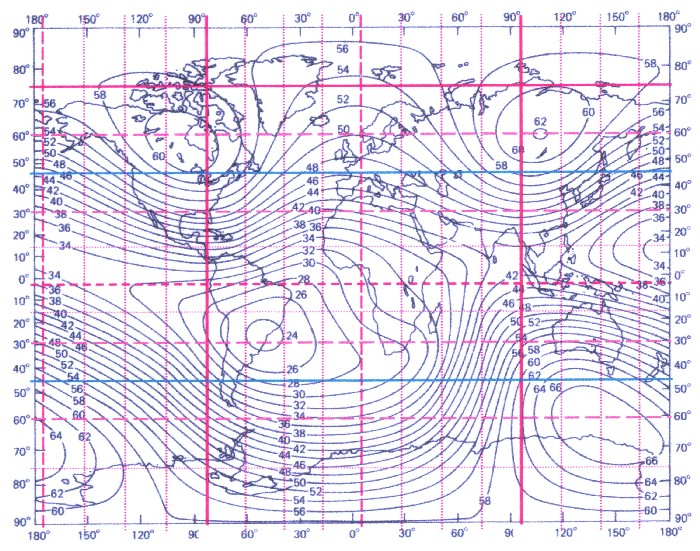| Abbildung 17.8 - Das C-Gitter |
| Das C-Gitter enthält somit alle Informationen über das Magnetfeld und über die Erdgestalt unter Berücksichtigung eines dreiachsigen Ellipsoids. |
17.6 - Das Bermuda Dreieck
| Seit dem Erscheinen der Bücher „Das Bermuda Dreieck“ 1974/75 und „Spurlos“ 1977 von Charles Berlitz haben sich um die dort zu beobachtenden Phänomene zahlreiche Gerüchte gerankt, die auch in der breiten Öffentlichkeit Aufmerksamkeit erzielt haben. Das Bermuda Dreieck liegt im atlantischen Seegebiet östlich der Halbinsel von Florida. |
 |
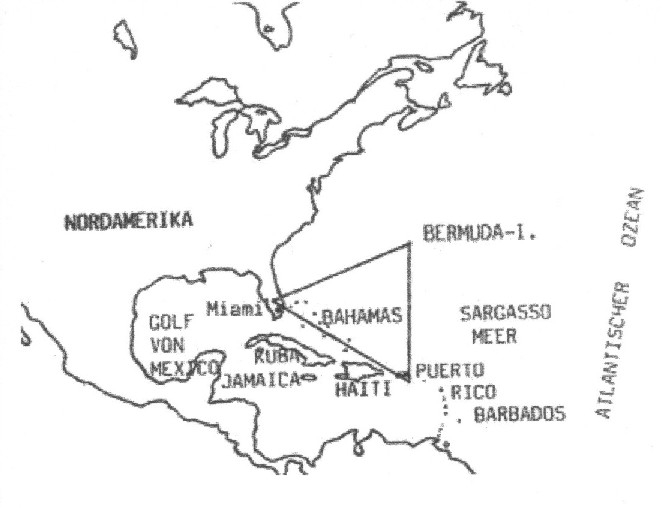| Abbildung 17.9 - Das Bermuda Dreieck |
| Die
Ergebnisse der Magnetfelduntersuchung des Autors
erbrachten Erkenntnisse, die eine Stellungnahme zu einem
der Phänomene des Bermuda Dreiecks ermöglichen. Und
zwar geht es um die bisher beschriebenen Fälle von mysteriösem
Kompassverhalten wie Kreiseln oder Schwanken der
Kompassnadel oder auch statische Missweisung. Vergleicht man die Lage des Bermuda Dreiecks mit dem C-Gitter (Abbildung 17.8) so erkennt man sofort, dass das Dreieck direkt am Hauptmeridian (λ = - 83,5 Grad West) des planetaren magnetischen Schwingungssystems liegt. Da sich um den Hauptmeridian herum die Extremalzone bis zu 15 Grad beiderseits ausweitet, liegt das Bermuda Dreieck also in der magnetischen Maximalzone dieses Planeten. Gleichzeitig läuft auch der 30te Breitengrad durch das Gebiet, und wie in Kapitel 17.3 zu sehen war, liegen hier zwei geometrisch ausgezeichnete Breitengrade. (siehe auch Abb.9.2, 9.5, 9.8 in Kapitel 9) Zieht man nun die Karte der jährlichen magnetischen Veränderung aus dem WMM 2005 („World Magnetic Model“ siehe auch Kapitel 2.2) heran (Abb. 17.10) und zeichnet den Hauptmeridian (mit seinen Maximalzonen) des planetaren magnetischen Schwingungssystems ein, so ergibt sich eine verblüffende Übereinstimmung: |
 |
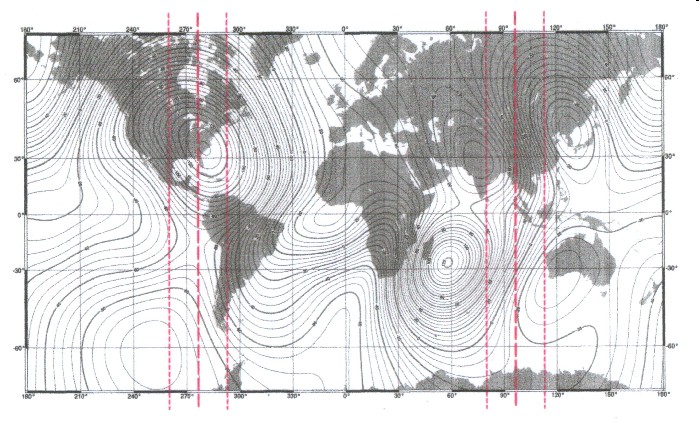| Abbildung 17.10 - Karte der jährlichen Veränderung mit Hauptmeridian - nach WMM 2005 |
| Es
existieren nur zwei Gebiete mit einem Maximum
an Änderung des Feldes. Ein Gebiet
liegt östlich der Spitze von Afrika, das andere Gebiet
deckt sich teilweise mit dem Bermuda Dreieck. Vergleicht man Abb. 17.10 mit Abb. 17.7 bzw. 17.8 so erkennt man, dass das Nordmaximum des tesseralen Feldes und auch ein Quellpunktbereich sich in unmittelbarer Nähe befinden (siehe auch Abb.9.11 in Kapitel 9). Da auch der Hauptmeridian des planetaren Schwingungssystem hier verläuft, ist die Konsequenz das Bermuda Dreieck als den einzigen Ort auf der Erde anzusehen, an dem die stärksten Fluktuationen im magnetischen Feld auftreten können. Diese Fluktuationen können sowohl temporär als Schwankungen vorkommen, als auch in der Intensität und Richtung der Feldanteile variieren. Dadurch sind Effekte wie Kreiseln oder auch Schwanken einer Kompassnadel, sowie statische Missweisung hier als durchaus plausibel anzusehen. Und das sind ja genau die Art von Kompasserscheinungen, von denen berichtet wird, dass sie im Bermuda Dreieck auftreten. (siehe Doppelband „Das Bermuda Dreieck“ von Berlitz und Valentine, Seite 19, 24, 35, 73, 76, 77, 80, 91, 92 bzw. „Spurlos“, Seite 16, 17, 24, 25, 30, 46) |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
