|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| German Version |
10 - Summary of the fourier analysis
10.1 - The longitude position of the extreme values
| How already, derived in
the chapter 4, the longitude positions of the
extreme values for the whole field can be shown by an
equation. This equation could be refined in chapter 9.5. Now it would be pointed out to the fact that this equation counts practically to all appearing extreme values of the magnetic field. |
|
|
|
| m is an element of the integers (...-3,-2,-1,0,1,2,3...) and λ0 = -13,5 degrees of west | |
| Because the zero point with λ0= -13,5 degree of west longitude and the value of Lundquist and Veis (see chapter 4.4) correspond, seen on a global scale well, so it can be ascertained: | |
| All
magnetic extreme values stand in relation to the equator axes of a three-axle ellipsoid |
10.2 - Evaluation of the extreme values
| If one looks at the earth
virtually from above, namely thus one looks down on the
north pole or the south pole and applies certain circles
of latitude (0, 30, 45, 60 degrees), one receives a
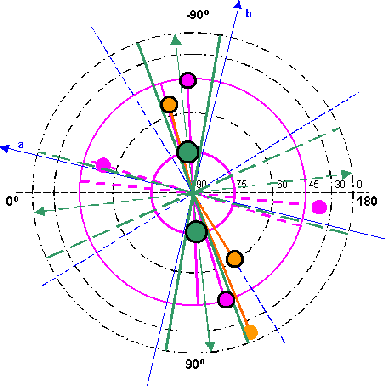
radial co-ordinate system. Mark of the axes for a three-axle ellipsoid (the blue cartesian co-ordinate system with λ0 = -13,5 degree of west) and registration of all magnetic extreme values found up to now produces both pictures 10.1 and 10.2. |
| The colours in it
signify: Green stands for the basic field ZS, Magenta for
the tesseral field and orange for the appearing extreme
values of the whole field from chapter 2.6. Die Farben darin bedeuten: Grün steht für das Grundfeld ZS, Magenta für das tesserale Feld und orange für die vorkommenden Extrema des Gesamtfeldes aus chapter 2.6. |
| North hemisphere | South hemisphere | |
 |
 |
|
| The values on the north hemisphere can be accommodated in a narrow zone (70-86 degrees of west). Likewise the values on the south hemisphere. | ||
 |
 |
|
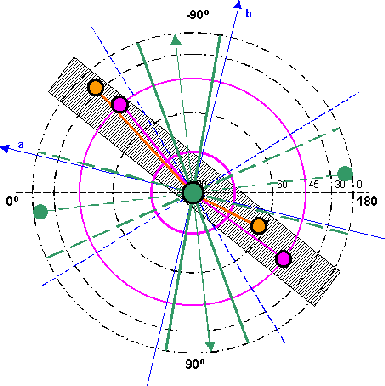
| From the illustration
10.1 arises: Practically all extreme values on the north hemisphere can be accommodated in a narrow zone by 55-90 degrees of west or 90-125 degrees of east. Merely both minima of the tesseral field form an exception here. From the illustration 10.2 arises: The extreme values on the south hemisphere can be likewise arranged in a narrow zone of 25-50 degrees of west or 130-155 degrees of east. The exception is formed here by both minima of the basic field ZS. The extreme zone on the north hemisphere is shifted about 35-40 degrees compared with the southern extreme zone. |
| In the book the
phenomenon of the movement is explained, namely with the
help of the maps of the vertical intensity and the
Inklination. Besides, even the place of the sturgeon source can be localised. |
10.3 - Basic fields
| Especially interesting in the fourier analysis is that between the tesseral portion of the earth magnetic field and the basic fields a narrow connection exists: Every term in the tesseral portion BT can be shown as a basic field. (see chapter 5) Here some examples to the illustration: |
 |
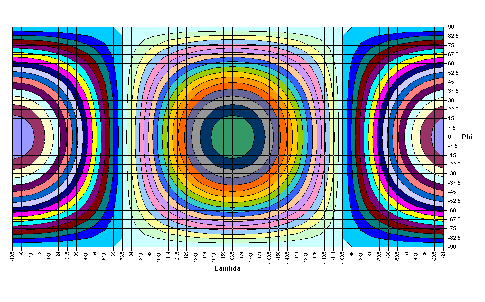-8,4184·cosλ·sinφ | |
 |
8,8172·cosλ·sin2φ | |
 |
-5,2834·cosλ·sin3φ | |
 |
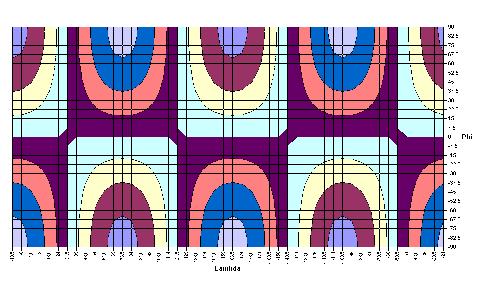-1,6626·cos2λ· sinφ | |
 |
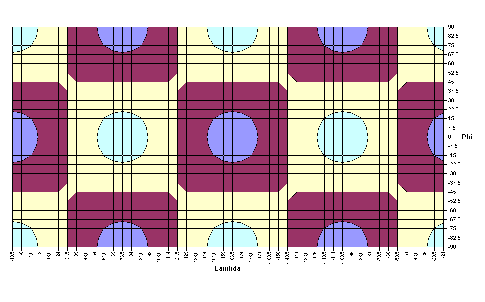0,6739·cos2λ·sin2φ | |
 |
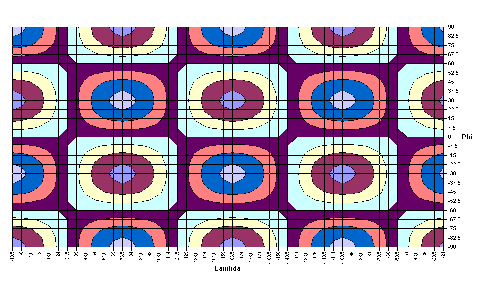1,6343·cos2λ·sin3φ |
| As at the examples or in
the equation for BT is to be seen, all
appearing terms of the tesseral part insist of spherical
harmonics how they also appear in the equation of Gauß (chapter 2.7). The tesseral portion of the
earth magnetic field consists of basic fields, i.e. from grid
structures similar to the Hartmann-grid. One can show the magnetic field of the earth from the sum of the tesseral part with the basic field ZS: |
| B = 47,2183 + BZS + BT μT (mükroTesla) |
| The consequence from it is: |
| The
external magnetic field of the earth can be completely
described by a sum of basic fields (grids) |
| The book to the website - The website to
the book at time is the book only in german language available |
||
|
|
| The Advanced Book: Planetary Systems |
| The theory, which is developed in this book is based on the remake and expansion of an old idea. It was the idea of a central body, preferably in the shape of a ball, formed around or in concentric layers.
Democritus was the first who took this idea with his atomic theory and thereby introduced himself to the atoms as fixed and solid building blocks. Is the atom used as a wave model, that allows to interpret concentric layers as an expression of a spatial radial oscillator so you reach the current orbital model of atoms. Now, this book shows that these oscillatory order structures, described by Laplace’s equation, on earth and their layers are (geologically and atmospherically) implemented. In addition the theory can be applied on concentric systems, which are not spherical but flat, like the solar system with its planets, the rings that have some planets and the moons of planets or also the neighbouring galaxies of the milky way. This principle is applicable on fruits and flowers, such as peach, orange, coconut, dahlia or narcissus. This allows the conclusion that the theory of a central body as a spatial radial oscillator can be applied also to other spherical phenomena such as spherical galactic nebulae, black holes, or even the universe itself. This in turn suggests that the idea of the central body constitutes a general principle of structuring in this universe as a spatial radial oscillator as well as macroscopic, microscopic and sub microscopic. |
|
