|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| German Version |
8 - Fourier analysis of the earth magnetic field
8.1 - Preparation to the Fourier analysis
| Starting point of the fourier analysis is the field
of the total intensity as it was already introduced in
the chapter 2–
Illustration 2.1 and is shown in Illustration
8.1 (IGRF
1980) once again. With these graphics a table was
generated for the values of the complete intensity. conditions: |
| Longitude: -180° ≤ λ
≤ +180° Latitude: -90° ≤ φ ≤ +90° |
 |
A table of
the values can be found here Table of earth field The whole field is disassembled in single cuts. Every cut proceeds along a circle of latitude. Besides, zero point is the beginning value of -13,5 degrees of west ascertained in the chapter 4. From +90 north to -90 south the cuts became invested in the distance of 7.5 degrees - this then produces 24 cuts. |
|
| Illustration 8.1 - World map of the magnetic total intensity |
| One submits every cut to
a linear (numerical) fourier analysis,
with the variable λ and the step
width 7.5 degrees, i.e. with 48
points per cut. A total of 1106 points
arise thus for the analysis of the earth field. (see also numerical harmonious analysis in " mathematics for engineers from Brauch, Dreyer, Haacke - page 490) As a basis of the whole analysis serves a numerical (linear) harmonious procedure as it is described in the book "Mathematik für Ingenieure" by Brauch/Dreyer/Haacke and also is known as an algorithm by Goertzel (and Reinsch). The linear numerical procedure functions with an angle from 0 to 360 degrees. For this first numerical harmonious analysis of the cuts along the parallels, so with the degree of longitude λ, the condition on the value area is fulfilled. Merely the parametre λ must be adapted. It is worth: |
 |
| This procedure delivers for a given numerical order, so here to the values of a cut, the suitable Fourier coefficients. With these coefficients the cuts can be shown as a sum of trigonometric functions. |
8.1.1 - Two-dimensional Fourier analysis
| Then 24 cuts by which the first Fourier analysis causes, can be shown in general so: |
 |
until |  |
| If one writes out these equations, the following picture arises: |
 |
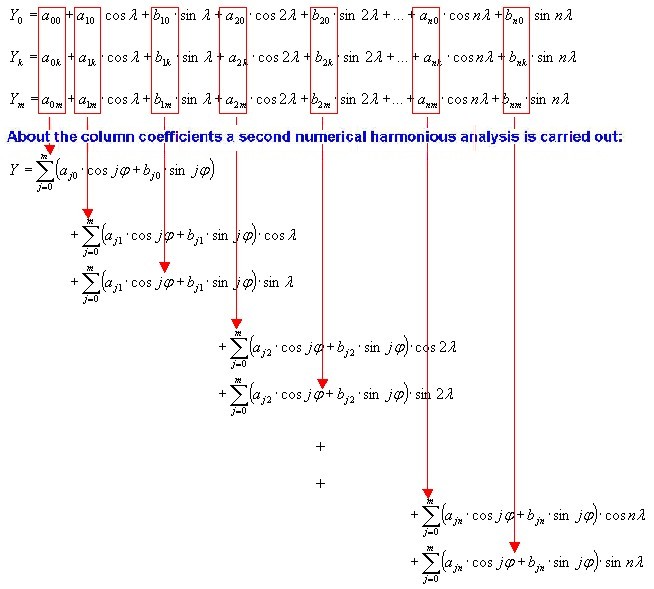| By the first numerical harmonious analysis occurs an equation system with m+1 formulas with in each case n+1 limbs owns. Then an other Fourier analysis, with the variables can be carried out about the columns of the coefficient matrix (with the Am und Bm) and the variable φ (Phi). This second numerical harmonious analysis delivers the final coefficients with the Aji und Bji. | |
 |
|
| If one separates the zonal, sectoral part from the tesseral portion, than arise for every point on the earth with the parametres λ, φ this formula: | |
 |
| Attention: in the book a misprint has appeared in this equation!!! | |
| The first Term for Y (zonal, sectoral part) can be still complemented so: | |
 |
 |
| Then the qualitative final equation can be shown for a point on the earth's surface so: |
 |
| There is
to be noted here that λ, φ do not show directly
the geographic coordinates, but are parametres, which
represent these coordinates. If one multiplies the clips, so merely Terme of sines and Cosines funktions appear, which are tied together multiplikativ with each other. Socalled spherical harmonics or grids. |
| The magnetic field of the earth can be described by a sum of grids |
8.2 - The quantitative result
| A quantitative evaluation of the given table of the earth magnetic field by means of the described numerical Fourier analysis, generated for the earth-magnetic flux density B, the following result: |
| all values in μT (mükrotesla) |
|
| As to be
seen the variable itself disassembled the magnetic field
in a static one, a sectoral (BS),
a zonal (BZ)
and a tesseral (BT)
portion (see chapter 5). There are only terms on in the equation like in the formula of Gauß (see chapter 2.7). Then it is worth: |
| B = 47,2183 + BZ + BS + BT µT (mükrotesla) |
| The book to the website - The website to
the book at time is the book only in german language available |
||
|
|
| The Advanced Book: Planetary Systems |
| The theory, which is developed in this book is based on the remake and expansion of an old idea. It was the idea of a central body, preferably in the shape of a ball, formed around or in concentric layers.
Democritus was the first who took this idea with his atomic theory and thereby introduced himself to the atoms as fixed and solid building blocks. Is the atom used as a wave model, that allows to interpret concentric layers as an expression of a spatial radial oscillator so you reach the current orbital model of atoms. Now, this book shows that these oscillatory order structures, described by Laplaces equation, on earth and their layers are (geologically and atmospherically) implemented. In addition the theory can be applied on concentric systems, which are not spherical but flat, like the solar system with its planets, the rings that have some planets and the moons of planets or also the neighbouring galaxies of the milky way. This principle is applicable on fruits and flowers, such as peach, orange, coconut, dahlia or narcissus. This allows the conclusion that the theory of a central body as a spatial radial oscillator can be applied also to other spherical phenomena such as spherical galactic nebulae, black holes, or even the universe itself. This in turn suggests that the idea of the central body constitutes a general principle of structuring in this universe as a spatial radial oscillator as well as macroscopic, microscopic and sub microscopic. |
|
