|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| German Version |
6 - Derivation of the wavelength
6.1 - Conditions
| The basic condition after chapter 5.2 is that a whole number of oscillations fits once around the earth and thus forms a standing wave, as a steady state. In a first attempt counts to the surface: | ||
The wavelength corresponds
to a certain distance on the circumference of the earth.
In the following illustration 6.1 the situation is
illustrated for an oscillation. |
||
 |
and |  |
| If one looks at this situation from the earth centre, a certain angle a can be assigned to every oscillation. | ||
 |
||
| Then all together as a basis appears: | ||
 |
||
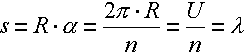| For reasons
of the illustration a factor has remained unnoticed, in
the previous representation, which must be included now
in the consideration: the ball figure of the
earth. It must be still taken into consideration that the wave propagation linearly takes place, and not along the curved earth surface. Hence, in the consequence it requires a modification of the basic equation. |
||
 |
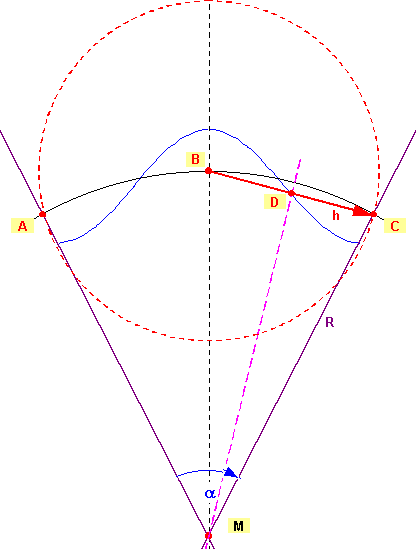| Illustration 6.1 - Wavelength and circumference |
6.2 - The derivation
| After the Huygens
principle the points A, B,
C in Illustration 6.1, so the extreme
points, serve as source points of the
standing wave. Electromagnetic waves spread out spherically from a point and if point B is the starting point, corresponds the distance BDC = h to the way of the wave. Because there is a steady state and it is enough to look the way of the wave from a source to the next source. |
 |
| The triangle MCD is right-angled in the point D and it counts: |
 |
 |
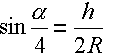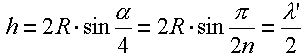| Change after lambda dash produces the corrected wavelength: |
 |
6.3 - The frequency equation
| The connection between wavelength and frequency is: |
 |
| With thus arises the equation for the earth frequencies: |
 |
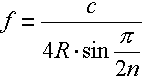| c
stands for the speed of light, R for the radius of the earth, n n for the number of oscillations Because the earth is, however, no
perfect sphere, there to the poles flattened. Here exist
two radii: the pole radius and the equator
radius. And
from it also result two (easily divergent of each other)
basic frequencies. |
| Pole radius :
11,79 Hertz Equator radius : 11,75 Hertz |
| The appearing difference
may seem unimportant at first sight. However, in case of
farther consideration a significant difference arises. In
the next chapter 7 this will become still clearly
recognizable in the subject sferics. Remark: Nikolas Tesla declared at his time that the earth frequency lies near 12 hertz. |
6.4 - A relation to the pole axis of the earth
| Another connection to the pole axis is given by the basic oscillation. If one declares for the first basic frequency the general solutions, these are: |
| n | f | Pole radius | Equator radius |
| 1 |  |
11,79 Hz | 11,75 Hz |
| 2 |  |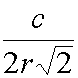
16,674 Hz | 16,618 Hz |
| 3 |  |
23,58 Hz | 23,5 Hz |
| For n=1 the general equation for the
wavelength is: lambda = 4R And one receives the identical result if a rod of the length of the Pole axis freely swung at both ends. As well as in the following illustration 6.2 shown. |
 |
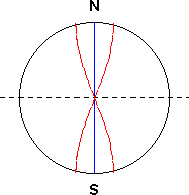| Illustration 6.2 - Earth and basic oscillation |
| Here the analogy is a
massive rod which both ends are free. If this rod is
moved now into oscillation, the basic oscillation
starting longitudinal flexural vibration corresponds to
the picture 6.2. (see also „Physik“ von Gerthsen, Kneser, Vogel – Kapitel 4.1.5) |
6.5 - The frequencies of the earth
| If one puts successively for n the values 1,2.3 ... in the above equation for the frequency, the basic frequencies of the earth arises. The following table contains the first 30 frequency oriented on the pole radius. |
| n | Pole radius |
| 1 | 11,7903 Hz |
| 2 | 16,6740 Hz |
| 3 | 23,5806 Hz |
| 4 | 30,8095 Hz |
| 5 | 38,1542 Hz |
| 6 | 45,5542 Hz |
| 7 | 52,9850 Hz |
| 8 | 60,4350 Hz |
| 9 | 67,8975 Hz |
| 10 | 75,3688 Hz |
| 11 | 82,8465 Hz |
| 12 | 90,3289 Hz |
| 13 | 97,8149 Hz |
| 14 | 105,3038 Hz |
| 15 | 112,7949 Hz |
| 16 | 120,2880 Hz |
| 17 | 127,7825 Hz |
| 18 | 135,2783 Hz |
| 19 | 142,7752 Hz |
| 20 | 150,2730 Hz |
| 21 | 157,7715 Hz |
| 22 | 165,2708 Hz |
| 23 | 172,7706 Hz |
| 24 | 180,2709 Hz |
| 25 | 187,7717 Hz |
| 26 | 195,2729 Hz |
| 27 | 202,7744 Hz |
| 28 | 210,2762 Hz |
| 29 | 217,7784 Hz |
| 30 | 225,2807 Hz |
| To this
basic frequency suitable harmonivs still appear, i.e. one
must form in addition only the integer multiples. (One calls harmonics as general integer multiples of an elective basic frequency) |
| In the book the frequencies are still declared which are oriented on the equator radius. |
6.6 - A further derivation
| In the book the derivation is still declared for a farther frequency equation. |
| The book to the website - The website to
the book at time is the book only in german language available |
||
|
|
| The Advanced Book: Planetary Systems |
| The theory, which is developed in this book is based on the remake and expansion of an old idea. It was the idea of a central body, preferably in the shape of a ball, formed around or in concentric layers.
Democritus was the first who took this idea with his atomic theory and thereby introduced himself to the atoms as fixed and solid building blocks. Is the atom used as a wave model, that allows to interpret concentric layers as an expression of a spatial radial oscillator so you reach the current orbital model of atoms. Now, this book shows that these oscillatory order structures, described by Laplace’s equation, on earth and their layers are (geologically and atmospherically) implemented. In addition the theory can be applied on concentric systems, which are not spherical but flat, like the solar system with its planets, the rings that have some planets and the moons of planets or also the neighbouring galaxies of the milky way. This principle is applicable on fruits and flowers, such as peach, orange, coconut, dahlia or narcissus. This allows the conclusion that the theory of a central body as a spatial radial oscillator can be applied also to other spherical phenomena such as spherical galactic nebulae, black holes, or even the universe itself. This in turn suggests that the idea of the central body constitutes a general principle of structuring in this universe as a spatial radial oscillator as well as macroscopic, microscopic and sub microscopic. |
|
