Frequencies and magnetic layers 2

	The magnetic field of the earth Lattice structures of the earth magnetic field

Impressum	Copyright © Klaus Piontzik


German Version

16 - Magnetic layers and frequencies 2

16.1 - Frequencies in the atmosphere for n<21

An oscillation spectrum forms the basis of the bowl construction of the earth
An oscillation spectrum forms the basis of the layer construction of the atmosphere
Both oscillation spectra are parts of the complete magnetic oscillation spectrum of the earth.

The earth is, about the magnetic field, with her inside and the atmosphere an oscillation unity.

If one understands the distances l' from the distance table as a wavelength of the accompanying hull or oscillation layer, suitable frequency can be assigned, as seen, to all distances. This also counts to the found averages of the extreme layers.

Frequencies in the atmosphere for n<21

Distance	Frequency	Height
km	Hz	km
6990,732	10,720	619,732
6976,920	10,741	605,920
6938,627	10,801	567,627
6887,079	10,882	516,079
6862,834	10,920	491,835
6843,795	10,950	472,796
6804,379	11,014	433,380
6775,855	11,060	404,855
6756,334	11,092	385,335
6742,948	11,114	371,949
6730,327	11,135	359,327
6688,747	11,204	317,748
6656,928	11,258	285,928
6636,025	11,293	265,025
6613,459	11,332	242,459
6593,773	11,366	222,774
6560,285	11,424	189,285
6539,935	11,459	168,935
6509,032	11,514	138,032
6480,640	11,564	109,641
6458,118	11,604	87,118
6437,634	11,641	66,635
6400,349	11,709	29,349

Then to all layer frequencies of the atmosphere counts:

Because certain layers of the atmosphere are connected with frequencies, so to electromagnetic activities, it should not surprise that events or processes by certain heights (weather forming) are afflicted with frequency or electromagnetic signals. The proof of the sferics confirms here the model.

16.2 - Frequencies in the earth for n<17

If one understands the distances l' from the distance table as a wavelength of the accompanying hull or oscillation layer, as in chapter 15 and 16.1 seen, suitable frequency also can be assigned to all distances within the earth from chapter 13.

Frequencies in the earth for n<17

Distance	Frequency	Depth
km	Hz	km
6355,76	11,79	15
6286,11	11,92	85
6191,29	12,10	180
6039,09	12,16	332
5982,18	12,52	389
5916,98	12,66	454
5766,16	12,99	605
5710,59	13,12	660
5667,58	13,22	703
5588,12	13,41	783
5359,12	13,98	1012
5258,39	14,25	1113
5105,49	14,68	1266
5022,45	14,92	1349
4953,86	15,13	1417
4914,98	15,25	1456
4855,23	15,43	1516
4781,63	15,67	1589
4678,69	16,02	1692
4483,91	16,71	1887
4357,42	17,20	2014
4177,23	17,94	2194
4026,54	18,61	2344
3937,52	19,03	2433
3851,37	19,46	2520
3710,71	20,19	2660
3589,32	20,88	2782
3508,23	21,36	2863
3410,02	21,98	2961
3374,53	22,21	2996
3203,35	23,39	3168
3045,35	24,61	3326
2971,18	25,22	3400
2899,27	25,85	3472
2690,05	27,86	3681
2587,64	28,96	3783
2485,39	30,15	3886
2351,41	31,87	4020
2162,10	34,66	4209
1989,48	37,67	4382
1897,28	39,50	4474
1735,07	43,19	4636
1632,65	45,90	4738
1464,59	51,17	4906
1304,91	57,43	5066
1137,12	65,91	5234
1071,01	69,98	5300
878,32	85,33	5493
776,94	96,46	5594
525,42	142,64	5846
423,39	177,02	5948
299,08	250,59	6072

Then to all layer frequencies of the earth inside counts:

Because certain layers of the earth inside are connected with frequencies, so to electromagnetic activities, it should not surprise that events or processes in certain depths (earthquake, plate tectonic) are afflicted with frequencies or electromagnetic signals.

16.3 - Frequency areas

All together arises from the preceding consideration:

The limiting frequency f_Erde shows practically the surface value of the earth. Because all living beings of the earth appear in a zone of about 10 km deeper or higher, the following statement can be effected:

All life on the earth is adapted to a frequency response of 11.7 - 11.8 hertz.

From the considerations of the preceding chapter also results that we are adapted to the
areas of 23,4-23,6 hertz as well as 46,8-47,2 hertz.

In consideration of the results from chapter 15.5 also count to the frequency areas that are orientated by the Schumann frequency (which are shifted around a quint).

All life on the earth is adapted to a frequency area of 11.7 - 11.8 hertz.

All life on the earth is also adapted to the frequency areas
from 7,8-7,9 hertz as well as 15,6-15,7 hertz and 31,2-31,5 hertz

Then with chapter 15.5 the following definition can be put up:

The earth frequency and the Schumann frequency generates common frequency which one can call
biological frequency

16.4 - The Adey window

In the middle of the 70s W.R.Adey and S.M. Bawin made experiments with cerebral tissue of chickens and cats. They irradiated the tissue with modulated VHF fields.

(see „Effects of modulated VHF fields on the central nervous system“ in „Ann N Y Acad Sci 247“ 1975 von Bawin, Kaczmarek und Adey / „Sensitivity of calcium binding in cerebral tissue to weak environ-mental electric fields oscillating at low frequency“ 1976 in „Proc. Natl. Acad. Sci. 73“ von Bawin und Adey / „Ionic factors in release of 45Ca2+ from chicken cerebral tissue by electromagnetic fields“ in „Proc Natl Acad Sci USA. 75“ 1978 von Bawin, Adey und Sabbot / „Models of long-range order in cerebral macromolecules: Effects of sub-ELF and of modulated VHF and UHF fields“ 1979 in „Radio Sci 14“ von Sheppard, Bawin und Adey / „Frequency and power windowing in tissue interactions with weak electromagnetic fields“ 1980 in „Proc. IEEE 68“ von Adey / „Tissue interactions with non-ionizing electromagnetic fields“ 1981 in „Physiol. Rev. 61“ von Adey / „Effects of weak amplitude-modulated microwave fields on calcium efflux from awake cat cerebral cortex“ in „Bioelectromagnetics 3“ 1982 von Adey, Bawin und Lawrence)

Adey and Bawin found with their investigations a narrow intensity area and frequency area in which the treated cells reacted. Nevertheless, beyond these areas occurred none or only minimum reaction. The experimentally ascertained frequency area is called, in the meantime, Adey window.

the Adey window

Illustration 16.1 - The Adey window

In the upper area of illustration 16.1 (on the right with A marked) an experiment is to be seen by Bawin from the year 1975. Besides, a frequency of 147 MHz with an ELF amplitude modulation was used. As a reaction to the radiotherapy the Ca-Ion-Efflux of the cells was measured.
In the lower part of illustration 16.1 (on the right with B marked) an experiment is shown by Adey and Bawin from the year 1976. However, with the same tissue type but in the frequency variable ELF fields.
Counts to part A of the illustration 16.1: In an area of 3 hertz to about 25 hertz a striking reaction is to be seen. Clearly is to be seen that from 6 hertz to 20 hertz a maximum is given in reaction.

A comparison with the frequency areas ascertained up to now from 16.3 shows that the areas of 7,8-7,9 hertz as well as 11,7-11,8 hertz and 15,6-15,7 hertz lie in the maximum area of the Adey window, if one understands the Adey window as a continuum.

The equation from chapter 6 delivers the earth frequency: for n=1 arose 11.75 hertz, for n=2 proved 16,62 hertz and for n=3 arose 23.5 hertz. Also this frequency lies well in the Adey window if one understands the Adey window as a continuum.

If one looks at the Adey window not as a continuum, but takes the discreet frequencies given in the illustration 16.1, one receives the following sequence (in hertz):

3 – 6 – 9 – 16 – 20 – 25 – 35

And around every frequency an area of ±0.8 hertz of tolerance exists.

From the equation in chapter 15.5 followed the table of the frequencies which owns earth frequency and Schumann frequency together. Besides, appears fo/3=fs/2=3,9307 Hz as the first smallest natural frequency which own earth frequency and Schumann frequency together.
From it results a sequence of frequency which are multiple of the basic frequency 3.93 hertz. (the first column in the table of chapter 15.5) The first nine frequencies are:

3,9307 - 7,8613 - 11,792 - 15,7227 - 19,6533 - 23,584 - 27,5147 - 31,4453 - 35,376

A part of this frequency agrees well with the frequencies of the Adey window. If the values of this sequence are halved arises:

1,9653 - 3,9307 - 5,896 - 7,8613 - 9,8267 - 11,792 - 13,7574 - 15,7227 - 17,688

If one sieves out now from all available frequencies those which are also included in the illustration 16.1 (part A), the following frequency spectrum arises for the Adey window:

3,9307 - 5,896 - 9,8267 - 15,7227 - 19,6533 - 23,584 - 35,376

Then this corresponds to the frequencies of the Adey window. One can show this frequencies also as rational multiples of the earth frequency and also the Schumann frequency. This proves the following table:

Frequenzies of the Adey-window 1

3,9307	5,896	9,8267	15,7227	19,6533	23,584	35,376
1/2 f_S	3/4 f_S	5/4 f_S	2 f_S	5/2 f_S	3 f_S	9/2 f_S
1/3 f₀	1/2 f₀	5/6 f₀	4/3 f₀	5/3 f₀	2 f₀	3 f₀

The frequency of the Adey window stands in harmonical relations
to the earth frequency respectively to the Schumann frequency.

The congruence between Adey window and earth frequency delivers a confirmation of the model derived up to now or the thesis that all life on this planet is adapted to certain frequency areas. The detailed treatise in addition takes place in the chapter 18.

16.5 - The Adey window and the Fibonacci sequence

With forming the half frequencies in chapter 16.4 resulted as smallest frequency f_m=1,9653 Hz

It is worth: f_m = 1/4 f_s = 1/6 f_o

If one compares fm to the frequency of the Adey window, all appearing Adey frequencies are multiples of 1,9653 hertz. If one takes into consideration this, the frequency can be shown as follows:

Frequenzies of the Adey-window 2

3,9307	5,896	9,8267	15,7227	19,6533	23,584	35,376
2 f_m	3 f_m	5 f_m	8 f_m	10 f_m	12 f_m	18 f_m

There originates thus the numerical sequence: 2 – 3 – 5 – 8 – 10– 12 – 18

And this corresponds to the, from mathematics known, Fibonacci-sequence with: 2 – 3 – 5 – 8 – 13 – 21
The fact that the Fibonacci sequence plays here a role, one can derive from the frequencies of the Adey window also directly:

The Adey-frequency sequence: 3 – 6 – 9 – 16 – 20 – 25 – 35
forming the half: 1,5 – 3 – 4,5 – 8 – 10 – 12,5 – 17,5
and rounding: 2 – 3 – 5 – 8 – 10 – 13 – 18

The Fibonacci sequence plays always a role where proportions with the golden section can be found. Hence, the Fibonacci sequence also seems in the nature, how with spiral growth of plants or also in the structure of seminal punches in flower states (sunflower). Also the Fibonacci sequence appears in the size of the populations, e.g., with rabbit and also bees.
It should not surprise to find this numerical sequence also in connection with the frequency of the Adey of window.

Tab.52: Frequenzies of the Adey-window as Fibonacci-sequence

3,9307	5,896	9,8267	15,7227	25,549
2 f_m	3 f_m	5 f_m	8 f_m	13 f_m

In the book is still given the equation by Binet for the Fibonacci sequence for the Adey window.

To the Fibonacci sequence and also to the equation of Binet a good arrangement and representation is to be found on the Internet in the "Wikipedia".
Caused by the discussion with the frequencies of the Adey window and the Fibonacci sequence, the installation of a second equation succeeded which allow to derive the discussed frequencies. Without other derivation only the result is announced here:

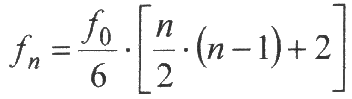The frequencies of the Adey window as Fibonacci sequence

This frequency sequence arises from it:

3,9307 - 5,896 - 9,8267 - 15,7227 - 23,584 - 33,411

What shows the frequencies of the Adey of window rather well.

back

home

next

	The book to the website - The website to the book at time is the book only in german language available

buy on Amazon

in over 1000 Online Shops

Production and Publishing company:
Books on Demand GmbH, Norderstedt

ISBN 9-783833-491269

Store price: 35 Euro

380 sides
72 pictures of it 51 in colour
55 tables
1530 literature references
1900 entries in the register of names

The Advanced Book: Planetary Systems

The theory, which is developed in this book is based on the remake and expansion of an old idea. It was the idea of a central body, preferably in the shape of a ball, formed around or in concentric layers. Democritus was the first who took this idea with his atomic theory and thereby introduced himself to the atoms as fixed and solid building blocks.
Is the atom used as a wave model, that allows to interpret concentric layers as an expression of a spatial radial oscillator so you reach the current orbital model of atoms.
Now, this book shows that these oscillatory order structures, described by Laplace’s equation, on earth and their layers are (geologically and atmospherically) implemented. In addition the theory can be applied on concentric systems, which are not spherical but flat, like the solar system with its planets, the rings that have some planets and the moons of planets or also the neighbouring galaxies of the milky way. This principle is applicable on fruits and flowers, such as peach, orange, coconut, dahlia or narcissus.
This allows the conclusion that the theory of a central body as a spatial radial oscillator can be applied also to other spherical phenomena such as spherical galactic nebulae, black holes, or even the universe itself. This in turn suggests that the idea of the central body constitutes a general principle of structuring in this universe as a spatial radial oscillator as well as macroscopic, microscopic and sub microscopic.

buy on Amazon