|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| Englische Version |
9 - Auswertung der Fourier-Analyse
9.1 - Der statische Anteil
| Laut der Fourier-Analyse beträgt der statische Anteil des Erdfelde 47,2183 μT. Der minimalste Wert des Feldes liegt bei 24 μT, der maximalste Wert beträgt 62 μT. Daraus erklärt sich, dass sich etwa 75 % des Feldes wie ein permanenter Magnet verhalten. |
9.2 - Der zonale Anteil
| Der zonale Anteil des Feldes entsteht durch die Auswertung der Mittelwerte in der Fourier-Analyse. Er enthält Terme die nur von der geographischen Breite φ (Phi) abhängig sind und lässt sich wie folgt darstellen: |
 |
 |
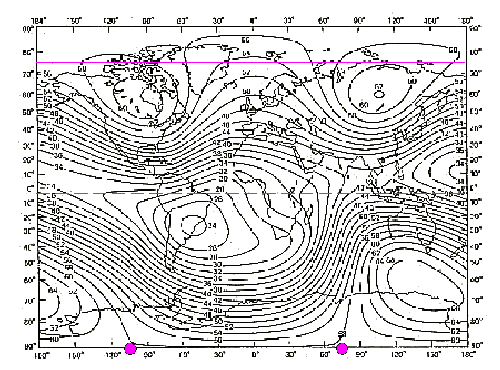Im Bild 9.1 ist zu erkennen, das sich um den
Nordpol herum eine Maximumzone bildet, und zwar bei φ=75
Grad. Etwa 2,8 Grad unterhalb des Äquators befindet sich eine Minimalzone. Und genau auf dem Südpol erhält man noch einen Maximalpunkt. Damit beruht das zonale Feld hauptsächlich auf einer 2er-Schwingung. Bedingt durch den Term 11,3642·cos2φ, der den grössten Anteil am zonalen Feld ausmacht. Und das dem Feld, zusammen mit dem permanenten Anteil, dann auch einen dipolähnlichen Charakter verleiht. |
|
| Abbildung 9.1 - zonaler Anteil des magnetischen Feldes |
9.3 - Der sektorielle Anteil
| Der sektorielle Anteil des Feldes entsteht durch die Auswertung der konstanten Glieder im tesseralen Anteil aus der Fourier-Analyse. Er enthält Terme die nur von der geographischen Länge λ (Lambda) abhängig sind und lässt sich folgendermaßen darstellen: |
 |
 |
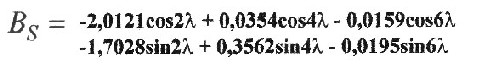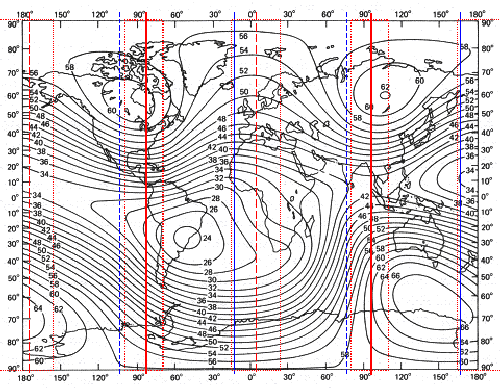Im Bild 9.2 ist zu erkennen, das sich neben
der kleinen Ellipsoidachse eine Maximumzone bildet, und
zwar bei λ=-83,5 Grad West und λ=96,5 Grad Ost. Die Minimumzonen liegen bei λ=5,25 Grad Ost und 174,25 Grad West. Die blauen Linien stellen die 0/180-Grad bzw. 90/270-Grad Meridiane eines dreiachsigen Ellipsoiden dar. |
|
| Abbildung 9.2 - sektorieller Anteil des magnetischen Feldes | ||
| Im Buch enthalten ist die Abbildung 9.3 die das sektorielle Feld in einer polaren Darstellung wiedergibt. |
Die Koordinaten für die Extremalzonen
| Name | Länge | Bereich |
| Maximum 1 | +96,5 Grad Ost | 80,25-110,25 Ost |
| Maximum 2 | -83,5 Grad West | -69,75-99,75 West |
| Minimum 1 | 5,25 Grad Ost | -15,5 West- +24 Ost |
| Minimum 2 | -174,75 Grad West | -156 West-+166,5 Ost |
9.4 - Grundfeld ZS
| Addiert man die Terme der zonalen und sektoriellen Anteile aus Kapitel 9.2 und 9.3, so entsteht das Grundfeld ZS. Es gilt: |
| BZS = BZ + BS |
 |
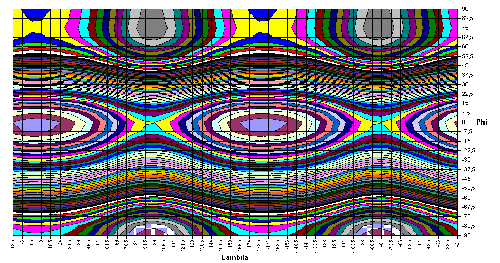Sichtbar wird, dass ein magnetischer Rücken
am Nordpol entsteht, während am Südpol nur eine
punktförmige Maximalzone vorhanden ist. In der Äquatorebene befinden sich zwei Minimalzonen und zwei Sattelpunkte. |
|
| Abbildung 9.4 - Grundfeld ZS | ||
 |
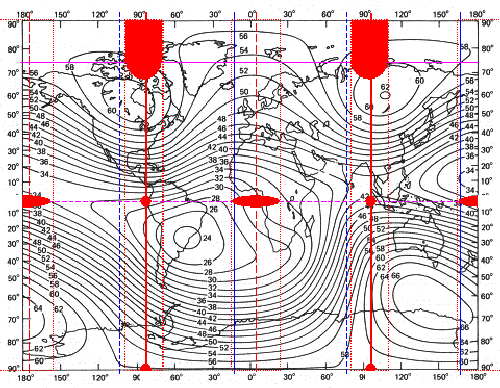Hier ist noch eine andere Art der
Darstellung des Grundfeldes ZS. Im Vergleich zum
Gesamtfeld und den Achsen für einen dreiachsigen
Ellipsoid. Gut zu erkennen ist der mangnetische Rücken im Arktisbereich. Sozusagen in Phase mit den Maximalpunkten befinden sich zwei Sattelpunkte in der Äquatorebene. Ebenfalls in der Äquatorebene befinden sich zwei Minimalzonen, die zu den Maximalwerten um 90 Grad verschoben sind, und daher am Hauptmeridian des dreiachsigen Ellipsoiden liegen. Alle Extremwertzonen liegen auf den Ecken eines Oktaeders |
|
| Abbildung 9.5 - Grundfeld ZS |
| Im Buch enthalten sind die Abbildung 9.6 und 9.7 die das Grundfeld ZS in einer polaren Darstellung wiedergeben. |
Koordinaten für die Extremwerte im Grundfeld ZS
| Name | Länge | Breite |
| Nord-Maximum | +96,5 Grad Ost | +75 Grad Nord |
| Anomalie | -83,5 Grad West | +75 Grad Nord |
| Minimum 1 | +5,25 Grad Ost | -5 Grad Sued |
| Minimum 2 | -174,75 Grad West | -5 Grad Sued |
| Süd-Maximum | 0 | -90 Grad Sued |
9.5 - Das GITTER ZS
| Trägt man lediglich die Linien für die Extremalzonen des Grundfeldes ZS in eine Weltkarte ein, so ergibt sich das erste Gitter für das Magnetfeld der Erde. |
 |
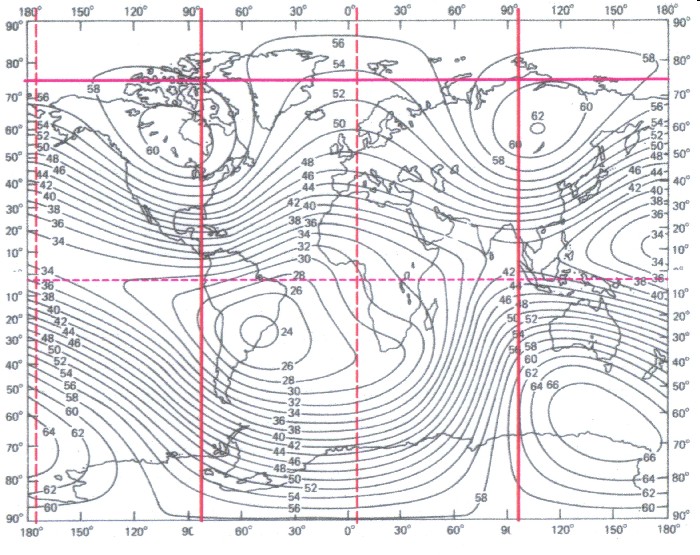| Abbildung 9.8 - Gitter ZS |
| Diese Gitterkonstruktion kann man dann als Gitter ZS oder auch als A-Gitter bezeichnen. |
| Die
Längenpositionen der Extremalzonen des Gitter ZS stimmt
mit den Werten des sektoriellen Anteils überein. Im
Gitter ZS ist die Maximumzone (rot) gut zu erkennen, und
zwar bei λ = -83,5 Grad West und λ = 96,5 Grad Ost. Die
Minimumzonen (rot gestrichelt) liegen bei λ = 5,25 Grad
Ost und bei λ = -174,25 Grad West. Das Grundfeld ZS und damit auch das Gitter ZS sind zu den Achsen eines dreiachsigen Ellipsoid (Nullpunkt nach Kapitel 4.4) um 18,75 Grad verschoben. 18,75 sind 5 mal 3,75 3,75 ist die Hälfte von 7,5. Damit lässt sich die Längenpositionsgleichung GL1 aus Kapitel 4.4 noch etwas differenzieren. Die Längenpositionen der Extremwerte bzw. –zonen des zonalen sowie des sektoriellen Anteils des magnetischen Feldes und damit auch die des Grundfeld ZS lassen sich dann durch folgende Gleichung darstellen: |
 |
| m
ist dabei Element der ganzen Zahlen
(...-3,-2,-1,0,1,2,3...) und λ0 = -13,5 Grad West Die Gleichung stellt eine Verfeinerung der Längenpositionsgleichung aus Kapitel 4 dar. |
9.6 - Die Lage der Kontinente
| Hauptsächlich aus den Abbildungen 9.2 und 9.8 lässt sich noch folgender verblüffender Zusammenhang ableiten: Die Lage der Kontinente hat direkten Bezug zu den Maximal- bzw. Minimalzonen des Grundfeld ZS bzw. des sektoriellen Feldanteils. |
|
|
| sektorieller Anteil des magnetischen Feldes | Gitter ZS |
| Amerika
liegt direkt in der westlichen Maximumzone. Die Landmasse
Sibiriens sowie die indonesische Landbrücke und Indien
liegen in der östlichen Maximalzone. Lediglich
Australien weicht etwas davon ab. Die Minimalzone, die an der Hauptachse des dreiachsigen Ellipsoid (Werte nach Lundquist und Veis) liegt, enthält Afrika und Europa. Lediglich die gegenüber liegende Minimalzone im pazifischen Ozean enthält keine Landmassen. Dafür dient sie als Trennlinie zwischen dem amerikanischen Kontinent und der eurasischen Landmasse. Daraus ergibt sich in der Konsequenz: |
| Die Lage der Kontinente steht in Relation zum sektoriellen Anteil des Erdmagnetfeldes |
9.7 - Nordlichtzone und magnetischer Rücken
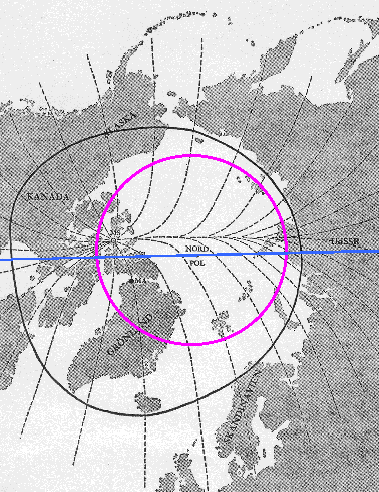
| Das folgende Bild 9.9 zeigt die Nordlichtzone (schwarzer Kreis) und die geomagnetischen Verhältnisse in der Arktis. Eingetragen sind jeweils die zonale (magenta Kreis) und die sektorielle (blaue Linie) Maximalzone. |
 |
Wie im Kapitel 9.2 gezeigt, liefert der
zonale Anteil einen Maximalwertwert bei 75 Grad
nördlicher Breite. Die gesamte zonale Maximalzone reicht
vom Pol bis zu etwa 67 Grad Breite. Dies stimmt gut mit
der Polarlichtzone überein. Durch Addition des zonalen mit dem sektoriellen Anteil lässt sich der magnetische Rücken in der Arktis erklären. Der magnetische Rücken stellt die Maximalzone des Grundfeld ZS dar. Vor diesem Hintergrund lässt sich folgendes Fazit ziehen: Das magnetische Feld am nördlichen Polarkreis wird hauptsächlich durch das Grundfeld ZS geprägt |
|
| Abbildung 9.9 - Arktis |
9.8 - Der tesserale Anteil
| Der tesserale Anteil enthält Terme die von der geographischen Länge λ (Lambda) und von der geographischen Breite φ (Phi) abhängig sind und lässt sich folgendermaßen darstellen: |
 |
 |
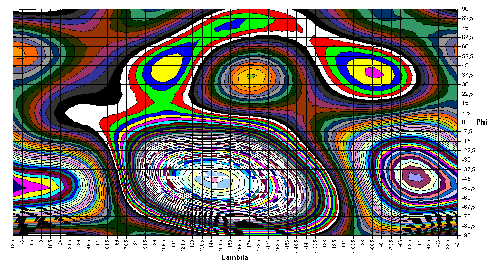Der tesserale Anteil des Erdmagnetfeldes Auffallend ist, das alle Extremwerte etwa bei ±45 Grad Breite liegen. |
|
| Abbildung 9.10 - tesseraler Anteil des Erdmagnetfeldes |
| Zeichnet man die Extremwerte des tesseralen Anteils (grün) in eine Karte mit der Totalintensität und den Achsen für ein dreiachsiges Ellipsoid (blau) mit einer 45 Grad-Teilung ein, so ergibt sich die folgende Abbildung 9.11: |
|
| Abbildung 9.11 - tesserale Extremwerte des Erdmagnetfeldes |
9.9 - Die Koordinaten der Extrema für das tesserale Feld
| Aus der Abbildung 9.10 ergeben sich die Koordinaten der Extremwerte: |
| Name | Breite | Länge |
| Nord-Maximum | +45 Grad Nord | -95,7685 Grad West |
| Süd-Maximum | -45 Grad Süd | +129,21 Grad Ost |
| Grosse Anomalie | +45 Grad Nord | +99,7395 Grad Ost |
| Minimum | -45 Grad Süd | +8,395 Grad West |
| Auf der Nordhalbkugel liegen alle Extremwerte annähernd auf einem Quadrat. Durch die 45 Grad Breite wird koordinatenmäßig in der Erde ein verdrehter Kubus bzw. ein verdrehtes Spat erzeugt. |
| Im Buch enthalten sind noch die Abbildungen 9.12 und 9.13 die eine polaren Darstellung des tesseralen Feldes liefern. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
