|
|
| Impressum | Copyright © Klaus Piontzik | |
 |
||
| Englische Version |
10 - Zusammenfassung der Analyse
10.1 - Die Längenposition der Extremwerte
| Wie schon, im Kapitel 4 abgeleitet, lassen sich die Längenpositionen der Extremwerte des Gesamtfeldes durch eine Gleichung darstellen. Diese Gleichung konnte in Kapitel 9.5 noch etwas verfeinert werden. Es sei jetzt darauf hingewiesen, das diese Gleichung praktisch für alle auftretenden Extremwerte des magnetischen Feldes gilt. | |
|
|
| m ist dabei Element der ganzen Zahlen (...-3,-2,-1,0,1,2,3...) und λ0 = -13,5 Grad West. | |
| Da der Nullpunkt von λ0 = -13,5 Grad West und der Wert von Lundquist und Veis (siehe Kapitel 4.4) global gesehen gut übereinstimmen, lässt sich feststellen: | |
| Alle
magnetischen Extremwerte stehen in Relation zu den Äquatorachsen eines dreiachsigen Ellipsoids |
10.2 - Auswertung der Extremwerte
| Betrachtet
man die Erde quasi von oben aus, und zwar so das man auf
den Nord- bzw. Südpol hinunter schaut und trägt
bestimmte Breitenkreise (0, 30, 45, 60 Grad) auf, so
erhält man ein radiales Koordinatensystem. Einzeichnen der Achsen für ein dreiachsiges Ellipsoid (das blaue kartesische Koordinatensystem mit λ0 = -13,5 Grad West) und Eintragen aller bisher gefundenen magnetischen Extremwerte ergibt die beiden folgenden Bilder 10.1 und 10.2. |
| Die Farben darin bedeuten: Grün steht für das Grundfeld ZS, Magenta für das tesserale Feld und orange für die vorkommenden Extrema des Gesamtfeldes aus Kapitel 2.6. |
| Nordhalbkugel | Südhalbkugel | |
 |
 |
|
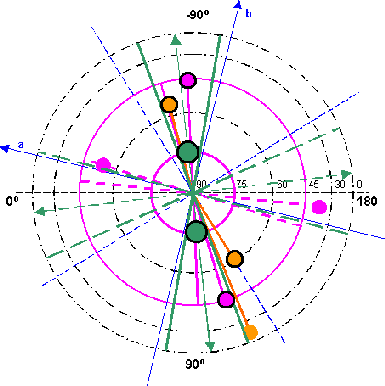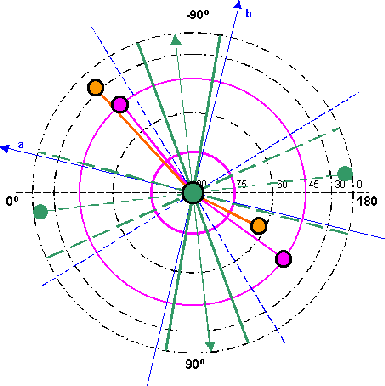| Die Werte auf der Nordhalbkugel lassen sich in einer schmale Zone (70-86 West) unterbringen. Desgleichen die Werte auf der Südhalbkugel. | ||
 |
 |
|
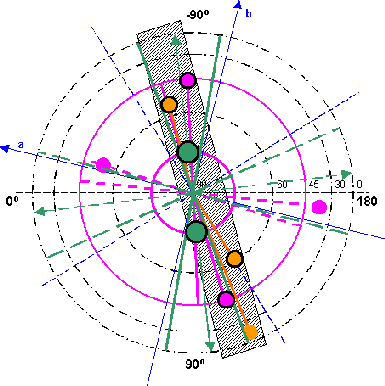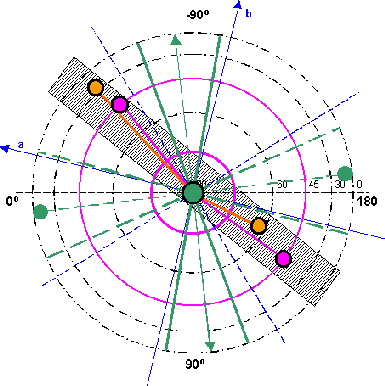| Aus der
Abbildung 10.1 ergibt sich: Praktisch alle Extremwerte auf der Nordhalbkugel lassen sich in einer schmalen Zone von 55-90 West bzw. 90-125 Ost unterbringen. Eine Ausnahme bilden hier lediglich die beiden Minima des tesseralen Feldes. Aus der Abbildung 10.2 ergibt sich: Die Extremwerte auf der Südhalbkugel lassen sich ebenfalls in einer schmalen Zone von 25-50 West bzw. 130-155 Ost einordnen. Die Aus-nahme wird hier durch die beiden Minima des Grundfeld ZS gebildet. Die Extremalzone auf der Nordhalbkugel ist um etwa 35-40 Grad gegenüber der südlichen Extremalzone verschoben. |
| Im Buch wird das
Phänomen der Verschiebung erklärt, und zwar anhand der
Karten der Vertikalintensität und der Inklination. Dabei kann sogar der Ort der Störquelle lokalisiert werden. |
10.3 - Grundfelder
| Besonders
interessant an der Fourier-Analyse ist, dass zwischen dem
tesseralen Anteil der Erdmagnetfeldes und den
Grundfeldern ein enger Zusammenhang besteht: Jeder Term
im tesseralen Anteil BT kann als
Grundfeld dargestellt werden. (siehe Kapitel 5) Hier einige Beispiele zur Veranschaulichung: |
 |
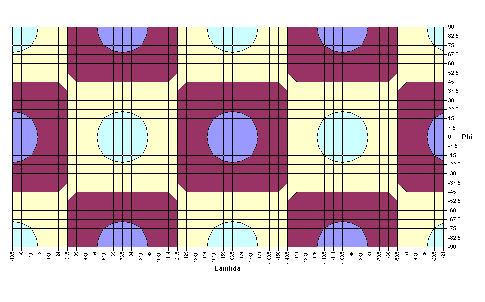
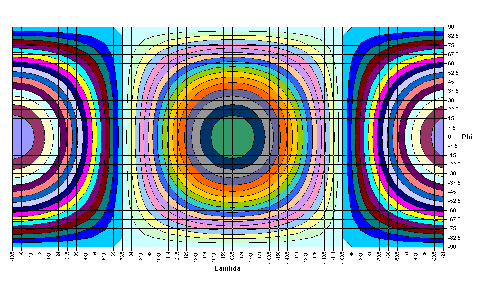-8,4184·cosλ·sinφ | |
 |
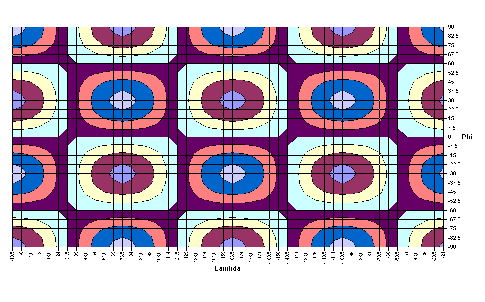
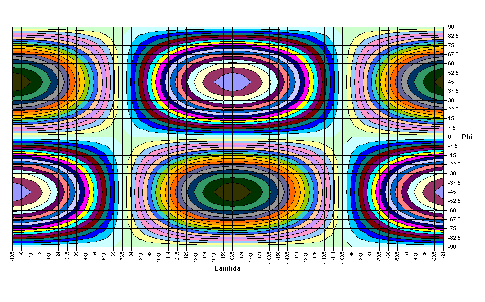8,8172·cosλ·sin2φ | |
 |
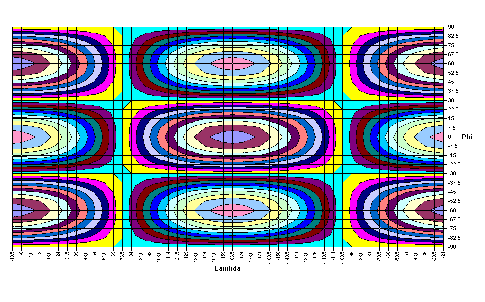-5,2834·cosλ·sin3φ | |
 |
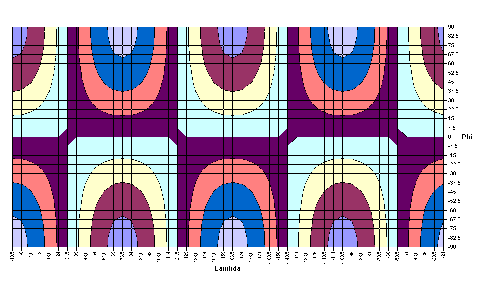-1,6626·cos2λ·sinφ | |
 |
0,6739·cos2λ·sin2φ | |
 |
1,6343·cos2λ·sin3φ |
| Wie an
den Beispielen bzw. an der Gleichung für BT
zu sehen ist, bestehen alle auftretenden Terme des
tesseralen Anteils aus Kugelflächenfunktionen, wie sie
auch in der Gleichung von Gauß (Kapitel 2.7) vorkommen. Der tesserale Anteil des Erdmagnetfeldes besteht also aus Grundfeldern (d.h. aus Hartmann-ähnlichen Gitterstrukturen). Das Magnetfeld der Erde kann man aus der Summe der tesseralen Anteils mit dem Grundfeld ZS darstellen: |
| B = 47,2183 + BZS + BT μT (mükroTesla) |
| Die Konsequenz daraus ist: |
| Das
äußere Magnetfeld der Erde lässt sich vollständig durch eine Summe von Grundfeldern bzw. Gittern beschreiben |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
